Inhaltsverzeichnis

Bemerkungen zum Thema Wachstum
- Quellen

Bemerkungen zum Thema Wachstum

link to an English translation: On Economic Growth

Vor allem in der politischen Ökonomie spielt Wachstum eine bedeutende Rolle. Die weit werbreitete Position ist, dass der Wohlstand zunehmen muss, damit es mehr zu verteilen gibt, denn die Begierde der Menschen ist unersättlich. Das ist die Grundposition der Schule der Wachstumsvertreter.

Es gibt nicht viele Kritiker - aber es gibt sie schon. Die haben begründete Kritik an der zentralen Bedeutung, die dem Wachstum gegeben wird. Meist sehen sie dann, ganz im Gegensatz zu den Wachstumvertretern, das Wachstum als solches als die entscheidende Ursache dafür, dass es Probleme wie z.B. die Treibhausgaszunahme gibt.

Hier werden ein paar Gesichtspunkte angeführt, die auf eine konkrete alternative Lösung bzgl. dieser Kontroverse hinweisen. Eine Lösung, die als Transformation in Fortsetzung eines Prozesses, der ohnehin schon läuft, entwickelt und umgesetzt werden kann. Die Analyse hat mehrere Teile:
(1) Die historische Aufbereitung: Das Wachstum war schon bisher gar nicht exponentiell…
(2) Die Rolle von Effizienzfaktoren (wie z.B. Produkt-Lebensdauern)
(3) Etwas elementare Mathematik: Die Summe der unendlichen geometrischen Folge konvergiert - doch was hat das mit dem Wachstum zu tun?
(4) Alles nur Theorie? Ein paar konkrete Umsetzungsansätze.

(1) Die historische Aufbereitung: Das Wachstum war schon bisher gar nicht exponentiell...

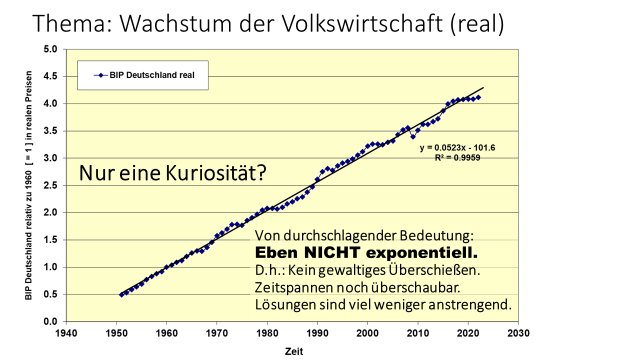
Das Wachstum war schon historisch nicht exponentiell; eher ziemlich gut linear. Das nimmt dieser Sache eine Menge Schärfe!

Kommuniziert werden bzgl. des Wirtschaftswachstums meist Prozentzahlen. Das ist anschaulich - und es spricht auch zunächst nichts dagegen. Dass allerdings die einmal gemessene Prozentzahl Jahr für Jahr in mindestens der gleichen Höhe weiter fortgesetzt werden muss - das folgt aus dieser Art Angabe natürlich nicht. Das ist vielmehr eine Frage der empirischen Forschung: Deren Ergebnisse gibt es, sie sind sogar leicht allgemein zugänglich (statistische Ämter). Ein wichtiger Punkt muss dabei beachtet werden: für die Realität, sowohl bzgl. des Wohlstandes als auch bzgl. der erforderlichen materiellen Ressourcen, ist nicht das nominale Brutto-Inlandsprodukt (BIP), sondern allenfalls das inflationsbereinigte ausschlaggebend²⁾. Das ist den statistischen Ämtern auch bewusst, daher gibt es die Daten als BIP-Zahlenreihen in realen Werten [Statista]. Die Grafik stellt dies am Beispiel Deutschlands für die Zeit nach dem II. Weltkrieg dar. Und da gibt es dann bereits zwei Überraschungen:

Ja, es gab ein stetiges und anhaltendes Wachstum - bis auf ein paar (wohlbekannte) kurzzeitige Einbrüche.
Das war aber keinesfalls exponentiell, sondern, mit überraschend überzeugender Korrelation, linear!

So schnell ließe sich das nicht, auch nicht mit gewaltigen Anstrengungen, in ein exponentielles Wachstum verwandeln. Auch wenn in der Politik das immer mal wieder gern versprochen wird. Kurzzeitige „Strohfeuer“ sind durchaus auch möglich - das geht dann aber regelmäßig auf Kosten der nachfolgenden Zeit nach dem übermäßigen Abfackeln des Feuers. Die Wachstumsvertreter mag das enttäuschen - und einige der Wachstumskritiker oft auch, denn es gibt unter diesen Umständen letztlich auch nicht die Gefahr eines gewaltigen unkontrollierbaren Überschießens³⁾. Und vor allem: Unter solchen Bedingungen bleiben die Zeitspannen für ein gesellschaftliches Handeln weiterhin überschaubar⁴⁾.

Fazit: Überschießende Wachstumserwartungen sind eine Illusion. Aber auch: Die Gefahr, dass das 'Wachstum als solches' in absehbarer Zeit zum fatalen Problem für die Gesellschaft werden sollte, besteht ebenfalls nicht akut. Die gesamte Problematik verdient es, etwas gelassener angegangen zu werden. Anders ausgedrückt: Lassen wir den Hyper-Hype mit dem unbegrenzt exponentiellen Wachstum oder seiner Forderung⁵⁾; und lassen wir auch das gelähmte Starren auf die „Schlange exponentielles Wachstum“⁶⁾. Befassen sollten wir uns stattdessen mit den konkreten Lösungen für die Probleme, die wir gesichert erkannt haben - wozu z.B. der Klimawandel gehört.

Wenn sich die Gesamtentwicklung weiterhin in geordneten (annähernd linearen) Bahnen vollzieht, dann haben wir Zeit. Zeit für eine vernunftgetragene Transformation auf ein nachhaltiges Wirtschaften⁷⁾. Ob und wie viel dabei das BIP dann auch noch wächst - das wird vor diesem Hintergrund eher zweitrangig, solange extreme Einbrüche und extreme Überhitzung vermieden werden. Das wird klar, wenn wir auch noch (2) und (3) hinzuziehen.

(2) Die Rolle von Effizienzfaktoren

Hier spreche ich, einzig wichtig in diesem Zusammenhang, nur Material- und Energie-Effizienz an. Das Thema Energieeffizienz wird auf den Seiten der Passipedia eingehend behandelt, z.B. hier. Dort wird auch gezeigt, dass im praktisch relevanten Bereich für fast alle Anwendungen die Energie-Effizienz-Verbesserung unbegrenzt möglich ist; ob sie letztlich bei einem sehr kleinen Restbedarfswert stagnieren wird, ist dabei im Grunde nicht relevant, weil dieser Wert in jedem Fall unter dem nachhaltig verfügbaren Energiestrom⁸⁾ liegt. Ich greife daher hier das Thema Materialeffizienz auf. Oft wird da argumentiert, dass da ja 'so sehr viel nicht zu holen' sei, denn eine bestimmte Mindest-Material-Menge für eine gegebene Aufgabe sei ja wohl offensichtlich. Selbst das ist keinesfalls so klar, wie es auf den ersten Blick erscheint. Aber es gibt noch einen weiteren Gesichtspunkt: Nämlich die Verweildauer, die ein einmal gewonnenes Material für diese Aufgabe in Nutzung bleibt. Die kann nämlich unterschiedlich lang sein. 'Beliebig' unterschiedlich lang? Das würde eine ziemlich philosophische Diskussion: Die Voyager-Raumsonden z.B. sind jetzt bereits seit September 1977 unterwegs; und sie laufen immer noch! Ich wage hier die These: Für die praktischen Fragen der Gegenwart können die Nutzungsdauern 'quasi' beliebig lang verlängert werden, solange es sich nicht um Verbrauchsmaterial handelt⁹⁾.

Wie gut ist denn dann „gut genug“?

Die nächste Überraschung: Das ist eine rein mathematische Frage. Wenn eine Aufgabe bisher mit einem System der Nutzungsdauer $t_N$ erledigt wird und das Wachstum $p$ beträgt¹⁰⁾, dann braucht die neue Lebensdauer neuer Systeme dieses Typs nur jetzt mehr als $(1+p)\cdot t_N - t_N = p \cdot t_N$ länger zu halten; sagen wir, die neue Lebensdauer ist $(1+\epsilon)$ mal $t_N$, dann ist $(1+\epsilon)$ ein typischer Effizienzfaktor. Dass der jedes Jahr erneut „aufmultipliziert“ werden kann, ist für die Anfangszeit unbestreitbar - auf Dauer natürlich eine Diskussion wert¹¹⁾¹²⁾. Die jährlich weiter erforderliche geförderte Materialmenge entwickelt sich dann nach

$\;\displaystyle q=\frac {1+p}{1+\epsilon} < 1 \;$

mit einem jährlichen Faktor $q$ kleiner als 1, also abklingend exponentiell. Das ist der entscheidende Punkt, wie mit Abschnitt (3) klar wird.

(3) Etwas Mathematik: Sogar die Summe der unendlichen geometrischen Folge konvergiert!

Das ist nicht neu, fast alle haben das irgendwann in der Schule gehabt - meist natürlich nicht mit der Tragweite diskutiert, die es für die Praxis hat; wie so oft bei mathematischen Erkenntnissen: Viele von denen sind sehr viel relevanter als es der meist trockene Mathematik-Unterricht erscheinen lässt; das kann an sehr vielen Stellen so richtig spannend sein!

Erstmal die Fakten: Sei $q$ ein Faktor mit Betrag kleiner als 1. Dann ist die 'unendliche Summe'(genannt: geometrische Reihe)

$1+q+q^2+q^3+...$

ein endlicher Wert. Wer die folgende Box mit den Formeln als zu herausfordernd empfindet, kann diesen Zusammenhang auch auf der hier verlinkten Seite veranschaulicht finden und die Box erst einmal überspringen.

Eingebürgert hat sich in der Mathematik die Schreibweise mit dem Summenzeichen $\sum$ dafür:

$\;\displaystyle { \sum_{n=0}^\infty {q^n} = \frac{1}{1-q} } \;$

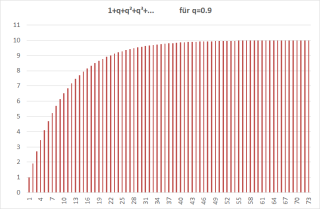
Da haben wir nun bereits die Lösung für diese 'unendliche' Summe angegeben, nämlich den Kehrwert von $1-q$. Ist $q$ z.B. 90%, dann ist $1-q=$0,1 und die unendliche Summe wird das 10-fache der derzeitigen Förderung an dem fraglichen Material; das reicht dann für die Versorgung in „Ewigkeit“. Die Grafik illustriert diese Summe für den Fall $q=$0,9 für bis zu N=73 Summenden; da ist das bereits sehr nahe an „10“, aber es ist immer noch Platz da für unendlich viele, ständig zügig kleiner werdende $q^n$ (den Beweis stecken wir in eine Fußnote¹³⁾ ).

Hier ist „Ewigkeit“($\infty$) selbstredend genauso praktisch irrelevant wie bei der Debatte um das niemals endende materielle exponentielle Wachstum: Wenn die Zeiten einmal bei einigen Jahrhunderten angekommen sind, lassen sich immer Lösungen finden, solange nur die „Bedarfs“werte nicht gigantisch hoch sind - was sie, gemäß der $q^n$ Entwicklung mit einem $q<1$ gar nicht sein können. Im Gegenteil: $q^n$ wird immer für irgendein $n$ unbedeutend klein, genau wie die dann noch folgenden Summanden. So klein, dass das für die Praxis unbedeutend ist, weil es dann nachwachsende Ressourcen¹⁴⁾ gibt, die das spielend abdecken. Nicht mehr gültig wird es in der Realität dann sein, wenn wir wirklich über 'unendliche Zeiten'¹⁵⁾ reden¹⁶⁾.

Kurz zusammengefasst: $q<1$ bzw. Effizienzzuwachs größer als Bedarfszuwachs löst somit tatsächlich das Wachstumsproblem.

Provokativ nochmal anders ausgedrückt: Wohlstandszunahme ist durchaus weiterhin erlaubt: Solange sie mit „Augenmaß“ erfolgt, eben über bessere Effizienz und nachwachsende Ressourcen 'finanziert' wird¹⁷⁾.

Ja, natürlich ist mir klar, dass das beiden „Lagern“ nicht passt: Den Wachstumsvertretern nicht, weil sie alles unterhalb von ewigem exponentiellem Wachstum als unsexy ansehen; und den Wachstums-Kritikern nicht, weil hier durchaus eine gemäßigte weitere Zunahme des 'Wohlstandes' zumindest denkbar erscheint.

Gehen wir mit offenem Geist an diese Fragen heran. Es wäre nicht das erste Mal, dass eine mathematische Analyse eine seit alters als 'unlösbar' angesehene Frage eben doch löst¹⁸⁾. Denn: Es gibt ihn eben doch, den technischen Fortschritt; allerdings: Erzwingen lässt er sich nicht und verantwortungsvoll einsetzen müssen wir ihn schon. Ich könnte Effizienzgewinne immer gleich wieder in übermäßig zunehmende Verschwendung stecken - es muss klar werden, dass das nur soweit geht, wie weiter $q<1$ bleibt. Aber einen „Stillstand“ bedeutet das eben gerade nicht¹⁹⁾. Wir können soviel wachsen, wie wir uns das ehrlich nachhaltig verdient haben - und dann müssen keine nicht-erneuerbaren Ressourcen darunter leiden. Das ist vernünftiges Wirtschaften im verallgemeinerten Sinn; und das ist dann auch ehrlicher Wohlstand, der nachhaltig verdient ist. Machen wir uns aber nichts vor: Derzeit sind wir von einer solchen Gleichgewichtswirtschaft noch weit entfernt - zu viele Jahrzehnte wurde die maßlose Steigerung des Konsums aus der Substanz voran getrieben; erst allmählich wird uns das nun bewusst. Die Umstellung wird anstrengend, aber es geht - und wir zeigen an relevanten Beispielen, wie.

(4) Alles nur Theorie?

Der hier zunächst abstrakt dargestellte Zusammenhang ist tatsächlich von hoher praktischer Relevanz. Auf Passipedia ist zu den konkreten Lösungen dafür schon viel verfügbar: Konkrete, bis zur Bauanleitung gehende Beschreibungen der Maßnahmen, die $q<1$ zumindest im Bereich der Energiesysteme als umsetzbar erweisen: Praxis der Energieeffizienz. Dass damit Zielwerte von $q<0,98$ erreicht werden, wird darin im Detail dargestellt²⁰⁾. Die Frage, ob die genannte Strategie auch über die zunächst betrachteten 50 Jahre ausgedehnt werden kann, lässt sich auch bereits heute positiv beantworten²¹⁾.

Weiter gibt es sogar bereits heute empirische Erfahrung, die wir hier für zwei Anwendungssektoren, nämlich den Verkehr und die Gebäudeheizung schon beleuchtet haben. Das fassen wir hier nochmals kurz zusammen.

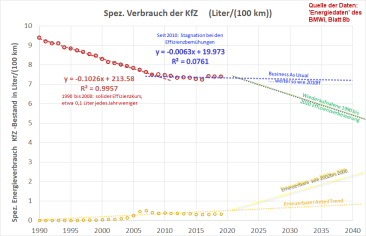Der spezifische Energiebedarf von Personen-Kraftfahrzeugen in Deutschland 1990 bis 2019 ist das Maß für die technische In-Effizienz der Autos. Bis etwa 2008 wurde die Effizienz tatsächlich jährlich um etwa 1 Zehntel Liter je 100 km verbessert. Seither ist jedoch praktisch nichts mehr passiert. Dabei wäre das ein relativ bequemer Weg, viele Probleme zugleich zu lösen. $q=$0,99 < 1 in diesem Fall. Technisch möglich ist die Verbesserung allemal - ein batterieelektrischer PKW 'braucht' nur ungefähr ein Viertel der Endenergie; wird die Ineffizienz eines immer noch bestehenden Anteils an fossiler Stromerzeugung mit berücksichtigt, bleibt immer noch ein um mehr als 50% reduzierter Verbrauch; je mehr Erneuerbare Energie ausgebaut wird, umso mehr nähert sich das an weniger als 30%. Diese 30% sind am Ende sogar problemlos vollständig erneuerbar zu erzeugen²²⁾.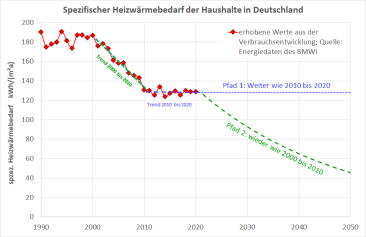

Vor 2010 waren die eingeleiteten Wärmeschutzmaßnahmen ziemlich erfolgreich, wie die grün gestrichelte Trendlinie 2000-2010 zeigt. In diesem Zeitraum kamen wir im Schnitt etwa 5 kWh/(m²a) jedes Jahr im spezifischen Verbrauch herunter, das waren mehr als 2,7% (jährlich!); $q=$0,973 < 1 in diesem Fall. Technisch und ökonomisch möglich ist die Fortsetzung in jedem Fall: Eine ordentlich durchgeführte EnerPHit-Sanierung reduziert den Heizwärmebedarf in jedem individuellen Fall auf unter 33 kWh/(m²a), das ist im Durchschnitt eine Reduktion auf ein Viertel und die Arbeitszahlen der Wärmpumpen erhöhen das zusätzlich. Wenn wir diese Verbesserungen über rund 30 Jahre verteilen, reicht das, um die angegebene Quote zu erreichen - und mit genau diesem Tempo haben wir das offensichtlich 2000 bis 2010 auch erfolgreich gemacht²³⁾.

Tatsächlich haben wir jeweils $q<1$ für über ein Jahrzehnt erfolgreich in diesen beiden Sektoren realisiert²⁴⁾.

Wir haben also bereits bewiesen, dass das, auch für eine ganze Volkswirtschaft, erfolgreich geht. Klar ist allerdings auch: Ganz automatisch und von selbst passiert das nicht, wir müssen es aktiv einleiten und dann auch wirklich durchführen.

Der zügige Ausbau der erneuerbaren Energie gehört selbstverständlich mit dazu: Damit sich die fallende Bedarfskurve und die steigende erneuerbare Erzeugung treffen können, und das nicht erst 2100²⁵⁾ sondern schon um rund 2050²⁶⁾.

Um noch ein wenig mehr positive Perspektive zu bieten: Ab rund 2050 ist auf diesem Weg eine 'Erneuerbare Überproduktion' von Energie möglich (über den Bedarf an Dienstleistungen hinaus). Die könnten wir dann z.B. wieder in „noch schnellere Autos stecken“. Besser wäre es aber dann, dass wir diesen Energie-Überschuss verwenden, um aktiv weiteres CO₂ aus der Atmosphäre zu holen; dass auch das möglich ist, ist ebenfalls demonstriert (sog. „direct air capture“, [DAC]). Das wird notwendig sein, um die schon aufgelaufenen Sünden der Vergangenheit zu korrigieren: Denn, wir haben heute bereits mehr CO₂ emittiert, als es für eine nachhaltige Entwicklung auf dem Planeten gut ist. Wenn wir uns dann weiter anstrengen, können wir sogar ein 1,5°C-Ziel bis 2100 immer noch erreichen. Aber allein auf Entscheidungen zu setzen, die erst in 25 Jahren getroffen werden können, halte ich für unverantwortlich²⁷⁾. Diese Überlegung zeigt eines: Lösungen, die eine Umstellung auf eine nachhaltige Entwicklung ermöglichen, gibt es. Es ist noch lange nicht 'alles verloren'.

Um nochmal auf die einführende Analyse zum in Wirklichkeit nur linear anwachsenden Brutto-Inlandsprodukt (das Diagramm unter (1)) zurück zu kommen: Wer (2) und (3) verfolgt und nachgerechnet hat, wird feststellen, dass beides auch ohne die Annahme, dass es gar kein auf Dauer exponentielles Wachstum gibt, auskommt; es wurde ja gerade selbst in (2) immer noch ein konstantes prozentuales Wachstum $p$ verwendet. Für (2) und (3) kommt es somit nur darauf an, dass der prozentuale Effizienzgewinn $\epsilon$ größer ist als dieses prozentuale Wachstum $p$. Dazu allerdings ist die empirische Erkenntnis des eben nicht exponentiellen sondern linearen realen BIP-Wachstums praktisch relevant: Da die Effizienzverbesserung (zumindest für die nächsten ca. 1000 Jahre) der absteigenden geometrischen Folge entsprechen kann, holt sie jeden linearen Zuwachs irgendwann ein. Derzeit liegt das reale Wachstum relativ zum derzeitigen BIP im Mittel bei rund 1,25%/a. Das ist bereits mit einem $\epsilon$ der gleichen Höhe (1,25%/a) abgefangen; wir haben schon mehr als das geschafft.

Worauf es somit ankommt: Alle Anstrengungen, die Energie- und Material-Effizienz zu verbessern! Das geht u.a. durch Wärmeschutz, Wärmerückgewinnung, Wärmepumpen, Low-Flow-Duschköpfe, effiziente Elektronik, Elektro-Traktion, Gegenstromöfen, längere Nutzungsdauern, Reparaturfähigkeit, Vorbeugung statt Schadenszulassung u.v.a.m. Damit tauchen wir innerhalb von wenigen Jahrzehnten unter die Grenze, die für ein nachhaltiges Wirtschaften unterschritten werden muss. Ab dann kann das weitere Wohlstandswachstum, so wir ein solches wollen, dem Zuwachs an erneuerbarer Erzeugung folgen; vielleicht haben wir dann aber auch soviel Spaß an den Effizienzansätzen gefunden, dass wir auch diese darüber hinaus fortsetzen und dann so noch mehr Raum für weiteres Wachstum schaffen²⁸⁾. Für die jetzt folgenden 30 bis 50 Jahre, die Zeit, auf die es ankommt, sind die Effizienzpotentiale für rund 3% Effizienzgewinn jedes Jahr schon heute nachgewiesen und in der Praxis demonstriert: Wir haben heute schon Häuser gebaut, deren Heizenergieverbrauch vernachlässigbar gering ist - und Fahrzeuge, die allein durch Muskelkraft auch 100 km/h schaffen. Und wir können mit dem allen immer noch besser werden, es gibt keine prinzipielle „Bestwertgrenze“.

Interessant in diesem Zusammenhang: Bemerkungen zum Fermi-Paradoxon.

Quellen

[Statista] Statistisches Bundesamt, dokumentiert in 'statista', Internet-Abruf am 13.12.2023 Index des Bruttoinlandproduktes bis 2022

²⁾

Ob das BIP ein gutes Maß für den Wohlstand darstellt, ist stark umstritten. Das ist allerdings ein anderes Thema, das wir bei Gelegenheit weiter diskutieren werden. Hier nehmen wir zunächst einmal das BIP als Maß ohne dies bzgl. der Wohlstandsfrage zu bewerten. Es ist sicher ein Maß für (offiziell abgerechnete) Wirtschaftsaktivitäten; somit im Grundsatz eher ein Maß für den Aufwand, den eine Nation unternimmt, um diese Aktivitäten durchzuführen.

³⁾

Wie das ja beim exponentiellen Wachstum wahrgenommen wird: Ab einem gewissen Punkt sieht dieses aus „wie eine Explosion“. Derweil ist es schon immer exponentiell - weil die absoluten Werte aber zunächst klein erschienen, hat das zunächst niemanden gekümmert.

⁴⁾

Natürlich auch das nur dann, wenn wir nicht einem Hyper-Hype von überzogenen unüberlegten 'schnell-schnell' Eingriffen zum Opfer fallen, welche eine hohe Gefahr von Fehlgriffen riskieren

⁵⁾

denn, dies geht ja ohnehin nicht

⁶⁾

eben weil es dieses auf Dauer auch ohnehin nicht gibt

⁷⁾

Allerdings haben wir nicht etwa Zeit, einfach so weiter zu wirtschaften, wie bisher: Der Wandel muss jetzt beginnen, wir wissen an den entscheidenden Stellen sogar sehr genau, wie; nämlich: Energieeffizienz verbessern und Erneuerbare Energie ausbauen.

⁸⁾

nämlich dem von der Sonne

⁹⁾

Die Differenzierung „Verbrauchsmaterial“ und Investitions-Material braucht eine weitere sorgfältige Betrachtung: Dies führt in der Regel auf die Notwendigkeit zur Vermeidung jeder Form von „Verbrauch“, der nicht allein auf nachwachsende Rohstoffe in einer zirkulären Ökonomie zurückgreift. So, wie das hier auch immer wieder am Beispiel Energie gezeigt wurde: Dabei ist die Effizienz mindestens so weit zu verbessern, dass die Rate der nachwachsenden Rohstoffe ausreicht, den konsumtiven Teil des Umsatzes zu decken (eben genau so, wie jedes Jahr auf den Feldern auch wieder soviel Kohl nachwächst, wie wir verspeisen). Zu behandeln ist dann natürlich, ob es für alle als „Verbrauchsmaterial“ identifizierten Ressourcen tatsächlich eine Lösung mit einem nachwachsenden Rohstoff gibt - das steht keinesfalls offensichtlich fest, es gibt dazu aber einen Hinweis: Die Ökosphäre der Erde hat auch komplexes Leben über viele Hundert Millionen erhalten. Wenn dazu nicht nachwachsende Ressourcen erforderlich wären, ist der Erschöpfungszeitraum jedenfalls so lang, dass wir diese Probleme nicht jetzt in jedem Einzelfall vollständig lösen müssen; wohl müssen wir es für einige der heute in übermäßigem Ausmaß industriell genutzten Rohstoffe (wie z.B. Iridium oder Helium) lösen.

¹⁰⁾

Faktor $(1+p)$ in der Dienstleistungsmenge; z.B. $p=$2,5% , dann ist $1+p=$1,025

¹¹⁾

diese „Dauer“, da sind aber Sorgen für Zeiten in „200 Jahren“ allerdings derzeit irrelevant; innerhalb von 200 Jahren wird klugen Menschen wieder eine gute Lösung einfallen. Innerhalb von nur 10 Jahren ist das so nicht erzwingbar - weshalb sich z.B. 'Lösungen' mit bisher unvertretbar nicht nachhaltigen Entsorgungsproblemen verbieten.

¹²⁾

Außerdem gibt es hier sicher einen Einwand seitens der Wachstums-Politik: Natürlich wird durch die längeren Lebensdauern das in BIP gemessene (und auch das Materialumsatz-) Wachstum reduziert. Trotzdem kann das Wachstum insgesamt p betragen, es können p mehr verkaufte Systeme sein - der Bestand nimmt dann dementsprechend zu. Das bedeutet, dass es sich dabei tatsächlich um einen echten Wertzuwachs handelt - während die reduzierten Abgänge infolge der längeren Lebensdauern in Wahrheit nur eine Ersatzbeschaffung sind; auch im ökonomischen Sinn ist die Verkürzung der Lebensdauer in Wahrheit kein wirklicher Wohlstandszuwachs: Sie erlaubt es allein, den Status quo aufrecht zu erhalten - aber mit höherem Aufwand. Verlängerung von Lebensdauern bedeutet daher auch ökonomisch eine Zunahme an Wohlstand, weil die gewonnenen Arbeitszeit für sinnvollere Dinge eingesetzt werden kann, oder, je nach gesellschaftlicher Priorität, auch zusätzliche Freizeit sein kann. Das ist ein ganz typisches Beispiel dafür, das höherer Eigennutz (nämlich durch kurze Lebensdauern erzeugte erhöhte Umsätze eines einzelnen Unternehmens) nicht identisch ist mit höherem Nutzen für alle, sondern ganz im Gegenteil, kontraproduktiv. Auch das muss nicht für alle auf der individuellen Ebene getroffenen Entscheidungen gelten; nur: Einen Automatismus gibt es nicht, weder in die eine, noch in die andere Richtung. Daher sind auch gesetzliche Vorgaben bzgl. Garantiezeiten und Reparaturfähigkeit sinnvoll. Wachstum durch verkürzte Lebensdauern ist in Wahrheit Scheinwachstum, sogar Wertverlust. Dafür gar politisch Anreize zu schaffen, reduziert die Gesamtleistungsfähigkeit der betroffenen Volkswirtschaft. Dieses Beispiel zeigt auch, dass das BIP, so wie es derzeit gemessen wird, kein vernünftiges Maß für den tatsächlichen Wohlstandszuwachs auch schon allein aus ökonomischer Sicht ist. Wenn kürzere Lebensdauern für ein Wachstumsziel verfolgt werden, ist das Ergebnis in Wirklichkeit genau das Gegenteil.

¹³⁾

Die geom. Reihe mit positivem $q<1$ konvergiert, weil der Wert immer mehr zunimmt, aber dennoch beschränkt ist. Den Wert der unendlichen Summe bekommen wir, wenn wir die Selbstähnlichkeit der Reihe beachten: multiplizieren wir $S=1+q+q^2+q^3+...$ mit $q$ selbst, dann erhalten wir $qS=q+q^2+q^3+...$; das sieht (fast) genauso aus wie die ursprüngliche Reihe, nur die führende „$1$“ fehlt. Ziehen wir die verschobene Reihe von der ursprünglichen ab, dann erhalten wir $S-qS=1+q-q+q^2-q^2+q^3-q^3+...=1$ und daraus sofort $S=\frac{1}{1-q}$.

¹⁴⁾

immer? Das ist noch einmal ein anderes Thema, das wir an anderem Ort weiter diskutieren werden. In voller Allgemeinheit ist das sicher nicht richtig - es sind nicht-substituierbare Materialien denkbar. Allerdings vertrete ich hier folgende These: Für die heute ökonomisch relevanten Ressourcen ist das nicht der Fall; hier gibt es regelmäßig eine, möglicherweise recht unterschiedlich umzusetzende Lösung gleicher Funktion, die in Fließgleichgewichte eingebettet werden kann, zumindest für relevante Zeitabschnitte oder die betreffende Bedarfsgröße ist 'verzichtbar', m.a.W. nicht überlebensnotwendig.

¹⁵⁾

was ist das? 100 Trilliarden Jahre? Nicht doch, immer noch viel, viel mehr

¹⁶⁾

Ob das in der Realität sinnvoll ist, das Universum so lange überhaupt existiert und wie es dann ungefähr aussehen wird, von all dem haben wir im Moment nicht die geringste Ahnung. Und ich gebe gerne zu, dass ich darüber zu Unterhaltungszwecken durchaus gerne spekuliere; halte das aber für nicht wirklich relevant. Dass die heutige Unwissenheit in dieser Frage zur Konsequenz habe, dass 'dann ja sowieso alles egal' ist, dem will ich hier aber deutlich widersprechen, denn das ist ein doppelter Fehlschluss: Einmal unterstellt eine solche Aussage nämlich, zu wissen, dass es 'irgendwann' ohnehin ein 'Ende mit Schrecken' gibt. Das lässt sich nicht ausschließen, aber wirklich gesichert wissen tun wir das heute (mindestens viele 100 Trilliarden Jahre davor) eben gerade noch nicht. Zum anderen lassen sich aus faktischen Erkenntnissen (reine Vernunft) ohnehin keine ethischen Forderungen ableiten (praktische Vernunft). Letztere brauchen immer ihr eigene Grundlegung.

¹⁷⁾

Aber auch nur dann! Denn, konsumieren wir mehr weg, als wir neu zusätzlich ermöglichen, geht es auf Kosten der Substanz.

¹⁸⁾

Ein Beispiel ist die „Quadratur des Kreises“ durch Archimedes. Oder die Quantenmechanik der Atomhüllen; die relativistische Formulierung der Mechanik; solche Beispiele ließen sich fortsetzen.

¹⁹⁾

Dass die Verkäufer mancher Verbrauchsstoffe (Öl, Gas aber auch Zement und Stahl) lieber mehr als weniger verkaufen wollen, versteht sich von selbst - da sollten wir auch nichts anderes erwarten. Das heißt aber nicht, dass wir allen Wünschen solcher Interessenvertreter unbegrenzte Interpretationshoheit bei den betroffenen Fragen zugestehen sollten. Natürlich wollen diese Effizienzgewinne am liebsten wieder gleich durch zusätzlichen Bedarf kompensiert sehen: Die größeren, schwereren Autos sind ein Beispiel. Das ist eben kein unvermeidlicher 'Rebound' - es ist das Ergebnis einer fleißigen Lobby sowie williger Politiker.

²⁰⁾

Es lässt sich auch mit einer kurzen überschlägigen Berechnung überprüfen: mindestens 2% pro Jahr muss die Effizienz im Gesamtsystem zunehmen. Das ist bei rund 75% Einsparung bei der Einzelmaßnahme gegeben, wenn die vollständige Umstellung nicht länger als rund 50 Jahre benötigt. Es kommt somit vor allem darauf an, dass die Einzelmaßnahme zu einer wirklich umfassenden Verbesserung führt: Das ist z.B. beim Umstieg auf E-Traktion bei Fahrzeugen der Fall, der spezifische Stromverbrauch liegt dann mit um 15 kWh/(100 km) um mehr als einen Faktor 4 unter dem heutigen durchschnittlichen Verbrauch (nämlich über 60 kWh/(100 km) an Benzin oder Diesel). Ähnlich verhält es sich mit der Umstellung beim Heizen: die Wärmepumpe allein bringt mindestens einen Faktor 2(Stromerzeugung im Winter durch Backup schon einbezogen, deswegen nicht 3 oder 3,5), die schrittweise Sanierung der Gebäude bringt mindestens einen weiteren Faktor 2. Diese Umstellungen sind alle jeweils innerhalb von rund 25 bis 35 Jahren vollständig zu bewältigen; allerdings: Das passiert nicht automatisch von selbst, es bedarf der Entscheidung, das auch umsetzen zu wollen.

²¹⁾

Wir gehen darauf z.B. auf der Seite zu Energieeffizienz ein; werden das aber künftig bzgl. konkreter weiter in der Zukunft liegender Potentiale noch erweitern. Für Zeiträume über 100 Jahre allerdings sind Überlegungen über das Prinzip hinaus kaum sinnvoll: Dann, gegenwärtig lassen sich die dann vorliegenden weiteren Erkenntnisse und die Umstände der menschlichen Zivilisation um 2120 keinesfalls zuverlässig abschätzen.

²²⁾

Damit taucht die Lösung dann in das Fließgleichgewicht des solaren Energiestroms auf die Erde ab und daher ist dann eine nachhaltige Eingliederung realisiert. Ab da können weitere Dienstleistungssteigerungen gleich auf zwei Wegen abgefangen werden: Durch Steigerung der erneuerbaren Energieerzeugung und durch weitere Verbesserung der Effizienz.

²³⁾

Damit wird dann auch in diesem Fall eine nachhaltige Lösung erreicht, weil der verbleibende Restbedarf problemlos erneuerbar gedeckt werden kann.

²⁴⁾

Übrigens lagen die jährlichen Reduktionsfaktoren dabei jeweils kleiner als 0,99. Das würde „allein“ dann noch rund 30 Jahre (Gebäude)bzw. 100 Jahre (PKW) Jahre benötigen, bis das nachhaltige Niveau erreicht ist. Weil zugleich aber auch die erneuerbare Erzeugung von Energie hochgefahren wird, werden sich die verbesserten Kurven für „erneuerbare Erzeugung“ und „durch Effizienz verringerten Verbrauch“ in der Zwischenzeit treffen; innerhalb von 25 bis 30 Jahren ist das leistbar - wenn wir uns gemeinsam dafür anstrengen. Funktioniert hat das jeweils bis zu dem Zeitpunkt, an dem uns die Lobbyisten erfolgreich eingeredet hatten, dass das alles gar nicht notwendig sei; Z.B. weil das russische Gas billig und sogar umweltfreundlich (Taxonomie!) sei.

²⁵⁾

nämlich zu spät

²⁶⁾

das ist so in jedem Fall zu schaffen, besser wäre es, dies noch schneller zu erreichen. Wozu viele weitere sinnvolle Dinge beitragen können, am einfachsten wäre dabei ein noch weiter gehende Effizienzverbesserung.

²⁷⁾

Denn, es ist auch klar: Ein Überschuss an Erneuerbarer Energie, das wird ab 2050 nur dann möglich, wenn diese auch sehr zügig ausgebaut werden und wenn zugleich die Effizienz in dem hier dargestellten Maß verbessert wird. DAC wird immer ein kleiner Beitrag bleiben, den Hauptanteil werden Effizienz und Erneuerbare heben müssen. Nur dann bietet uns ab 2050 auch wenig DAC die Chance, die Situation weiter zu verbessern und dann ein Tool verfügbar zu haben, mit dem das Klima auf dem Planeten dauerhaft stabil bleiben kann.

²⁸⁾

Wohlgemerkt: derzeit darf die zunehmende Effizienz eben gerade nicht ausschließlich in materielle Umsatzzunahmen gesteckt werden; schließlich müssen wir jetzt vor allem erst einmal von der eingetretenen weit überzogenen Naturausbeutung herunter kommen. Die Gefahr eines dann sog. Rebound besteht übrigens in der Realität nicht: Wir hatten das Thema Rebound-Effekt schon einmal aufgearbeitet.