Dies ist eine alte Version des Dokuments!

Inhaltsverzeichnis

Die Stirling-Maschine

Die Stirling-Maschine

Worum geht es in diesem Kapitel?

Wir wollen hier eine Wärmekraftmaschine in ihrer prinzipiellen Funktion behandeln. Eine Wärmekraftmaschine ist eine Maschine, die (zumindest einen Teil) der Wärme aus einem Wärmereservoir in mechanische Arbeit verwandelt. Das geht, wie die hier behandelte Maschine konkret beweist.

Damit werden wir schon einen ersten Nutzen aus dem Kapitel gezogen haben: Das ist der grundsätzlichen Aufbau eines Wärmekraftwerks.

Diese Maschine (ein thermodynamisches System) entnimmt Wärme aus einem Reservoir mit hoher Temperatur $T_h$ ¹⁾. Die Erfahrung hat immer wieder bestätigt, dass für eine solche Wärmentnahme noch ein zweites Reservoir mit einer kühleren Temperatur $T_c$ gebraucht wird²⁾, an das die Maschine regelmäßig den ganzen Rest der im heißen System abgeholten Wärme abgibt; eben den Rest, der nicht in Arbeit umgewandelt wird. Das kann sogar mit den Kenntnissen, die wir bereits haben, verstanden werden: Erst dann, wenn es ein zweites System mit einer niedrigeren Temperatur gibt, kann Wärme überhaupt vom heißen System abfließen; von dem so „angelockten“ Wärmestrom kann auf raffinierte Art ein Teil in mechanische Arbeit umgewandelt werden - wie, werden wir gleich sehen. Damit haben wir eine weitere Erkenntnis:

Wärmekraftmaschinen brauchen neben einer Wärmequelle auch eine Wärmesenke³⁾.

Das ist aber längst nicht alles, was wir mit dieser Maschine anfangen können: Es stellt sich nämlich heraus, dass jeder einzelne Ablauf beim Betrieb dieser Maschine (trotz des 2. Hauptsatzes!) auch in die umgekehrte Richtung laufen kann; diese Maschine ist, wie es in der Fachsprache heißt, reversibel. In dieser umgekehrten Richtung entnimmt die Maschine Wärme aus dem kälteren Reservoir⁴⁾ und führt diese Wärme zusammen mit der aufgebrachten mechanischen Arbeit an das heiße Reservoir ab. Damit haben wir gleich zwei praktisch bedeutende Maschinen gewonnen:

Den Kühlschrank: dem kältere Reservoir kann aktiv Wärme entnommen werden, es wird gekühlt. Und…

Die Wärmepumpe; dem heißeren Reservoir wird aktiv Wärme zugeführt, die zu einem großen Teil aus dem kälteren Reservoir stammt, aber auch die aufgewendete Arbeit enthält.

Diese beiden alternativen Nutzungen der Stirling-Maschine machen jeweils etwas, das nach der einfachen Intuition 'unvorstellbar' erscheint - in einem heißen System aus einer kälteren Umgebung heraus Wärme abziehen! Auf den allerersten Blick scheint es sogar, dass das der als 2. Hauptsatz formulierten Erfahrung widerspreche. Hier zeigt sich ein weiteres mal, wie wichtig eine klare Formulierung der Sachverhalte ist: Der zweite Hauptsatz sagt nicht, dass die Wärmeentnahme aus einem kälteren System nicht möglich sei. Er sagt nur, dass ein solcher Vorgang „nicht von selbst“ stattfindet und dass es nicht das einzige Ergebnis eines Prozesses sein kann: In unserem Fall geschieht die Wärmeentnahme auch nicht „von selbst“ sondern technisch bewerkstelligt mit der Stirling-Maschine; und zu deren Betrieb als Wärmepumpe wird mechanische Energie benötigt - die von irgendwoher bereitgestellt werden muss; dort fehlt sie dann, das ist das weitere Ergebnis des Prozesses. Damit eignet sich der Stirling-Prozess (in beide Richtungen) zur Präzisierung dessen, welche physikalischen Bedingungen dafür gegeben sein müssen und welcher minimale Aufwand dafür erforderlich ist, ein kaltes System doch weiter zu kühlen.

Aus Sicht der physikalischen Erkenntnis ist die Kombination dieser umgekehrt herum laufenden Maschine mit der ursprünglichen Maschine hoch interessant: führen wir beide Prozesse nacheinander durch, so sind alle Systeme (die Wärmekraftmaschine, die Wärmepumpe und beide Reservoire) hinterher in genau dem gleichen Zustand wie am Anfang.

Der ideale Stirling-Prozess ist genau so ein reversibler Prozess, der den von Natur aus eigentlich „irreversiblen“ Wärmetransport von $T_h$ nach $T_c$ reversibel macht. Ideal durchgeführt, wird der Wärmetransport dadurch 'verlustfrei'. Es wird nämlich genau soviel mechanische Arbeit gewonnen⁵⁾ wie wir hinterher wieder brauchen, um mit der gleichen Maschine im umgekehrten Ablauf die Wärme wieder zurück zu holen⁶⁾. Das ist somit

Ein exzellentes Beispiel für sehr hohe (im Grenzfall ideale) Energieeffizienz.

Es ist zugleich ein Tool, mit dem

Grundlegende Fragen der Thermodynamik behandelt und am Ende sogar quantitative Aussagen dazu hergeleitet werden können.

Wirklich, das ist eine ganze Schatztruhe, die wir damit erschließen. Das schönste daran aber ist:

Die hier beschriebene Maschine kann⁷⁾ tatsächlich in der Praxis gebaut werden. Dies wird klar, wenn wir die Erklärung zum Aufbau und zum Betrieb des Stirlingmotors - wie unten dargestellt - betrachten.

Das Foto ganz oben zeigt z.B. einen Eigenbau einer Stirling-Maschine von Pedro Servera. Im Internet gibt es eine Reihe von Beschreibungen zu „wir bauen uns einen Stirling-Motor“, z.B. hier; 'Stirling Engine - Made In An Hour'. Oder, ein einfaches Demonstrationsmodell kann auch bestellt werden (suche nach „Stirlingmotor“; hier wird das Modell erklärt: Stirling-Modell).

Die Bestandteile der Stirling-Maschine

Wir behandeln hier zunächst die Motorfunktion der Maschine. Diese benötigt zum Betrieb zwei weitere Systeme: Ein Temperaturreservoir mit einer hohen Temperatur $T_h$ („heiß“) und ein Reservoir mit einer niedrigeren Temperatur $T_c$ („kalt“. bzw. „cool“). Diese Systeme heißen Reservoire, weil sie, 'egal was passiert', ihre Temperatur halten. Insbesondere auch dann, wenn ihnen Wärme zugeführt bzw. entnommen wird. Eine 'Vorstellung' dazu ist, sich deren Wärmekapazität als extrem groß (quasi-unendlich) zu denken, dann macht ein wenig entnommene Wärme an der Temperatur kaum etwas aus; es ist aber auch eine technologische Realisation möglich, indem von einem geregelten Wärmeerzeuger immer genau die Wärme wieder zugeführt wird, die gerade entnommen wurde. Das ist die Methode, die bei realen Kraftwerken regelmäßig realisiert ist⁸⁾.	_{heißes (oben, rot) und kaltes Reservoir (blau)}
Zylinder Wir setzen einen Zylinder ein, in dem sich ein Arbeitsgas befindet. Als Arbeitsgas verwenden wir ein Gas, das in dem Temperaturbereich einem idealen Gas nahe kommt: Oft wird hier Helium benutzt und das kann in sehr guter Näherung zwischen Temperaturen von -150°C und 2000°C als ideales Gas angesehen werden. Durch das Gas ist nun ein Wärmetransport zwischen den Reservoiren möglich. „Von allein“ findet der nur von der höheren Temperatur zur niedrigeren Temperatur statt. Wir werden gleich sehen, welchen technischen Trick wir anwenden, um das Gas gezielt zu transportieren.	_{Arbeitsgas im Zylinder}
Arbeitskolben Wir setzen einen Arbeitskolben in den Zylinder ein. Der kann reibungsfrei (!) im Zylinder gleiten, sitzt aber absolut gasdicht. Damit kann das Gasvolumen innerhalb des Zylinders eingestellt werden: Schieben wir den Arbeitskolben hinauf, wird das Gas komprimiert und der Druck⁹⁾ steigt; bewegt sich der Kolben nach unten, dann expandiert das Gas und der Druck fällt. Das alles geschieht „langsam genug“, so dass das Gas überall oberhalb des Kolbens den gleichen Druck aufweist¹⁰⁾. „N(ord)…S(üd)“ seht auf dem Kolben, weil wir die Bewegung magnetisch steuern wollen. Die Arbeit für die Kolbenbewegung wird hier magnetisch ein- oder ausgekoppelt. Das geschieht z.B. durch eine elektrische Spule, die um den kalten Teilsektor des Arbeitszylinders gewickelt ist. Alternativ kann die Bewegung auch mechanisch z.B. über eine Pleuelstange von außen durchgeführt bzw. abgegriffen werden. Wir stellen diesen mechanischen Teil der Maschine hier nicht dar¹¹⁾.	_{Arbeitskolben}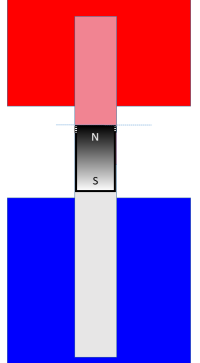
Hier ist ein Beispiel für den Arbeitskolben bei der Arbeit: Die „isotherme Expansion“¹²⁾ beim heißen Temperaturniveau ist im Gang. Der Kolben hat sich gegenüber der letzten Zeichnung so bewegt, dass das Volumen um d$V$ zugenommen hat. _{Infobox: zugehörige Gleichungen. Kann auch übersprungen werden} Aus d$V=A_q\cdot$d$s$ ($A_q$ ist der Querschnitt des Arbeitskolbens, d$s$ das Wegstückchen, das der Kolben zurücklegt) lässt sich durch Multiplikation mit dem Druck $p$ die Arbeit, die das Gas an den Kolben vermittelt, berechnen: d$w=F$d$s=pA_q\cdot$d$s=p$d$V\;$ Die Arbeit wird nach außen geleistet ¹³⁾. Wegen der Energieerhaltung müsste die Innere Energie des Gases um genau diesen Betrag abnehmen und die Temperatur des Gases dadurch fallen; das wird dadurch kompensiert, dass eben genau dieser Betrag vom Gas dem heißen Reservoir als Wärme entzogen wird: d$Q_I=$d$w_I$.	_{Expansion leistet Arbeit}
Jetzt kommt der angekündigte Trick! Wie können wir das Gas zwischen dem heißen und dem kalten Teil verschieben? Dazu dient ein Verdrängungskolben, der gerade groß genug ist, den heißen Bereich (und auch, alternativ, den kalten Bereich) im Zylinder zu füllen. Setzen wir diesen Verdrängungskolben an der richtigen Stelle in den Zylinder ein, so bleibt dem Arbeitsgas keine andere Möglichkeit als das Volumen im nicht verdrängten Teil des Zylinders. Freilich muss das Gas dazu durchaus am Verdrängungskolben vorbei kommen - oder, durch ihn hindurch - dafür ist der Kanal in seiner Mitte eingezeichnet. Da strömt das Gas reibungsfrei hindurch¹⁴⁾. Und, im Idealfall ist auch das Volumen im inneren dieses Kanals vernachlässigbar klein¹⁵⁾.	_{Verdrängungskolben}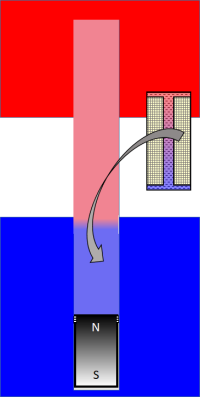
Der Verdrängungskolben lässt sich kräftefrei verschieben¹⁶⁾. In der nebenstehenden Zeichnung wird der Verdrängungskolben nach oben (also in den heißen Bereich hinein) verschoben. Er verdrängt das heiße Gas dort, es strömt durch den Kanal im Kolben auf die kalte Seite. Und hier kommt ein genialer Trick: der Kanal ist mit feinkörnigem wärmespeicherndem Material 'gefüllt', natürlich so, dass das Gas da immer noch mechanisch weitgehend ungehindert hindurchkommt. Da das Material in der Temperatur vom Boden bis zum Dach des Zylinders in der Temperatur von der des unteren auf die des oberen Reservoirs zunimmt, kann das Arbeitsgas sich beim Durchströmen jeweils an die Temperatur der Seite, auf die es wechselt, anpassen. Ein solches Teilsystem nennt sich „Regenerativ-Wärmeübertrager r-WÜ“ oder einfach „Regenerator“; diese WÜ finden in der Praxis auch bei der Wärmerückgewinnung Einsatz. Nun kennen wir alle Bestandteile der Maschine und können uns deren Arbeitsweise im Betrieb als Motor anschauen: Das erfolgt Schritt für Schritt in der nächsten Tabelle.	_{Verdrängungskolben im Einsatz}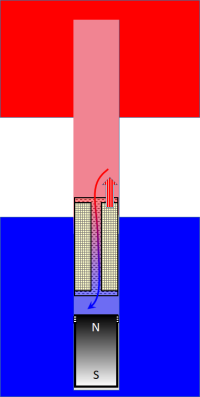

Der Prozess in Einzelschritten: Stirling-Maschine als Motor

Isotherme Expansion bei hoher Temperatur (Teilprozess I) Das Arbeitsgas dehnt sich hier durch Wärmeaufnahme aus dem Reservoir mit der hohen Temperatur aus: bei hohem Druck auf dem Kolben¹⁷⁾ wird Arbeit nach außen geleistet. Die Energie dafür kommt zunächst aus der Inneren Energie des Arbeitsgases, das sich diese aber aus dem Reservoir mit der hohen Temperatur gleich wieder abholt (weil wir den Teilprozess durch sehr gute thermische Kopplung an das Reservoir bei $T_h$ isotherm halten und damit bei konstanter Innerer Energie). Der Druck im Arbeitsgas ist auf jedem Teilstückchen der Expansion proportional zur Temperatur $T_h$ des heißen Reservoirs. Damit muss auch die Summe aller Arbeitsbeiträge im Teilprozess I proportional dazu sein: $w_I=C_{Maschine}\cdot T_h$ und die Wärmeentnahme aus dem Reservoir ist genau gleich hoch: $Q_I=w_I.$¹⁸⁾	_{Arbeitsprozess bei $T_h$}	_{Diese dritte Spalte kann ein Leser, für den dies „neue Inhalte“ sind, beim ersten Lesen erstmal überspringen. Hier kommt die mathematische Formulierung der zuvor erklärten Sachverhalte. Die quantitativen Ergebnisse dieser Experimente sind natürlich ohne die zugehörigen Gleichungen nicht zu bekommen}¹⁹⁾ Für ein kleines Teilstück der Expansion d$V$ haben wir die geleistete Arbeit schon weiter oben bestimmt: d$w=p \;$d$V$ Wir setzen darin die nach p aufgelöste Allgemeine Gasgleichung²⁰⁾ $\; \; p=\frac{Nk_B T_h}{V}$ ein: d$w=\frac{Nk_B T_h}{V} $d$V$ Diese kleinen Arbeitsbeträge lassen sich nun Schritt für Schritt zwischen $V_1$ und $V_2$ aufsummieren, sprich integrieren, das Ergebnis ist die gesamte geleistete Arbeit im Teilprozess I: ${\displaystyle w_I=\int_{V_1}^{V_2} d w=\int_{V_1}^{V_2} \frac{Nk_B T_h}{V}dV=Nk_B T_h \ln \frac{V_2}{V_1}.}$ Wieso? ⟶²¹⁾
Hier ist allein der Verdrängungskolben in Aktion: Er verdrängt das Gas im aus dem heißen Raum (Teilprozess II). Besonderer Trick: Der Regenerator nimmt dabei die Wärme auf, die bei der Abkühlung des Arbeitsgases frei wird. Das Volumen bleibt hierbei konstant, die Fachleute nennen dies einen „isochoren“ Prozess²²⁾. Daher wird dabei auch keine Arbeit geleistet. Bemerkung: Es handelt sich hierbei um eine „ideale“ Wärmerückgewinnung in das Speichermedium des Regenerators, 100% der bei $T_h$ höheren Inneren Energie des Gases gegenüber $T_c$ wird aufgenommen. Im idealisierten Gedankenexperiment (idealer Prozess) geht das.²³⁾	_{Verdrängung des Gases vom heißen in den kalten Raum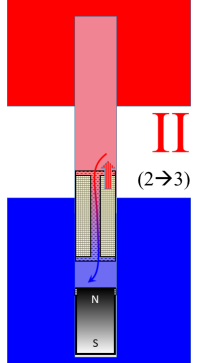}	Ergänzung noch zum letzten Teilprozess: Durch die Berechnung unter Verwendung der idealen Gasgleichung haben wir die Arbeit quantitativ bestimmen können. Sie ist tatsächlich proportional zum Temperaturniveau des heißen Reservoirs. Der Proportionalitätsfaktor $C_{Maschine}$ ist das Produkt aus Molekülzahl N, der Konstante $k_B$²⁴⁾ und dem Logarithmus des Verdichtungsverhältnisses $\frac{V_2}{V_1}.$ Nun die Zahlen zum Teilprozess II: Da hier das Volumen konstant ist, leistet das Gas keine Arbeit nach außen d$w_{II}$=0. Es wird aber auf die Temperatur $T_c$ abgekühlt; dabei gibt es Innere Energie in Form von Wärme an den Regenerator ab: $Q_{II}=\frac {f}{2} Nk_B \cdot (T_h - T_c).$ Der Regenerator speichert diese Wärme bis zum Teilprozess IV. (f ist die Zahl der Bewegungsoptionen für die Molekülart, genannt „Zahl der Freiheitsgrade“. In jeder Bewegungsoption verteilt sich je Molekül $\frac {f}{2}k_B T$ an innerer Energie im zeitlichen Mittelwert. Ist das Arbeitsgas Helium (wie oben beispielhaft erwähnt), so ist f=3 weil es drei unabhängige Raumrichtungen gibt, in die sich die Atome bewegen können.)
Jetzt ist das gesamte Arbeitsgas kalt und lässt sich (bei niedrigerem Gasdruck) leichter komprimieren. Dies erfolgt im Teilprozess III: Isotherme Kompression bei der niedrigen Temperatur. Das Arbeitsgas wird hier (durch Krafteinwirkung!) vom Kolben komprimiert; dabei muss dem Kolben natürlich Arbeit von außen zugeführt werden. Die Energie davon kommt zunächst der Inneren Energie des Arbeitsgases zugute, das diese aber gleich durch Wärmeableitung an das Reservoir mit der kühleren Temperatur abführt. Der Druck im Arbeitsgas ist auf jedem Teilstückchen der Expansion proportional zur Temperatur $T_c$ des kalten Reservoirs. Damit muss auch die Summe aller Arbeitsstückchen im Teilprozess I proportional dazu sein: $w_{III}=-C_{Maschine}\cdot T_c$ und die Wärmeabgabe an das Reservoir ist genau gleich hoch: $Q_{III}=w_{III}.$ Das Minus-Zeichen zeigt die diesmal umgekehrte Richtung des Energietransfers an: Hier muss äußere Arbeit aufgebracht werden.	_{Die Kompression kostet mechanische Arbeit; weil sie aber mit dem kalten Gas bei konstant $T_c$ durchgeführt wird, weniger Arbeit als zuvor bei der Expansion 'im heißen' geliefert wurde.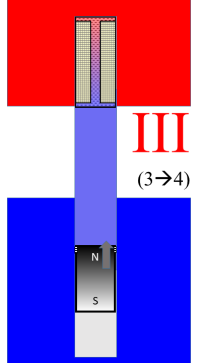}	Für ein kleines Teilstück der Kompression d$V$ ist die Arbeit d$w=p$d$V$ Mit der Allgemeine Gasgleichung wird das wie schon bei Teilprozess I d$w=\frac{Nk_B T_c}{V} $d$V$ Und wieder summieren wir die Schrittchen alle auf, diesmal vom größeren Volumen $V_2$ bis herunter zu $V_1$. Das Ergebnis ist die gesamte Arbeit im Teilprozess III: ${\displaystyle w_{III}=\int_{V_2}^{V_1} d w=\int_{V_2}^{V_1} \frac{Nk_B T_c}{V}dV=Nk_B T_c \ln \frac{V_1}{V_2}.}$ Der Logarithmus des Kehrwertes ist gleich dem Negativwert des Logarithmus, eben $-\ln \frac{V_2}{V_1}.$ und die Proportionalitätskonstante ist genau die Gleiche (!) wie beim Teilprozess I. Es ist also $w_{III}=-C_{Maschine}T_c.$ (wie schon in der ersten Spalte erkannt). Die hier benötigte Arbeit ist um $C_{Maschine} (T_h-T_c)$ kleiner als die im Teilprozess I gewonnene Arbeit. Wir gewinnen also im Netto Arbeit.
Nun haben wir vollständig komprimiertes Gas, es ist aber immer noch kalt. Jetzt schieben wir es einfach unter konstantem Volumen in den heißen Raum zurück (Teilprozess IV); das macht wieder der Verdrängungskolben, ohne Arbeitsaufwand. Zudem wird beim Strömen durch den mit dem Regenerator gefüllten Kanal das Arbeitsgas mit der vom letzten isochoren Prozess (II) gespeicherten Wärme auf die hohe Temperatur erwärmt. Die gespeicherte Wärmemenge passt gerade: Es ist die gleiche Masse an Gas und die betragsmäßig gleiche Temperaturdifferenz. Die Maschine ist jetzt wieder genau im Anfangszustand und der Stirling-Motor-Prozess kann jetzt beliebig oft wiederholt werden. Veränderungen gibt es aber in der 'Umwelt': Es wird Wärme aus $T_h$ entnommen, Abwärme in $T_c$ abgeführt und die Differenz $w_{tot}=C_{Maschine}(T_h-T_c)$ als Arbeit verfügbar gemacht.	_{Verdrängungskolben in den kalten Maschinenteil verschoben: Das Gas entweicht in den heißen Raum, der Druck steigt entsprechend kontinuierlich an.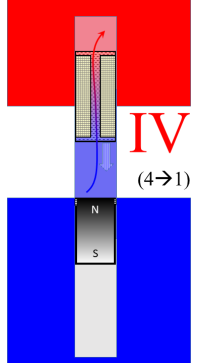}	Im Teilprozess IV ist wieder das Volumen konstant, das Gas leistet daher keine Arbeit nach außen d$w_{IV}$=0. Es wird nun auf die Temperatur $T_h$ erwärmt; dabei nimmt es Wärme aus dem Regenerator auf: $Q_{IV}=-\frac {f}{2} Nk_B \cdot (T_h - T_c).$ Das ist genau die Wärme, die der Regenerator aus dem Teilprozess II gespeichert hat. In der Summe aus den Teilprozessen II und IV wird nach außen weder Wärme noch Arbeit ausgetauscht. Und, am Ende ist der Regenerator wieder in genau dem gleichen Zustand „1“, ebenso wie das Arbeitsgas (also die ganze Maschine wieder zurück am Anfang); daher nennt die Fachwelt das auch einen „Kreisprozess“²⁵⁾. Geändert haben sich drei Dinge: Einmal ist Wärme $Q_I$ aus dem Reservoir $T_h$ abgeflossen. Zum zweiten ist Wärme $Q_{III}$ an das kühlere Reservoir abgeführt worden²⁶⁾; und zum dritten ist die Arbeit $w_{tot}=w_I + w_{III}= C_{Maschine} (T_h - T_c)$ über den Kolben nach außen abgegeben worden. Die Maschine arbeitet! Und gewinnt diese Arbeit aus der Wärmeentnahme vom höheren Niveau, muss dazu aber als eine Art „Tributzahlung“ eine zusätzliche Wärmeentnahme aus dem oberen Reservoir ins untere abtreten.

Der Prozess im Druck-Volumen-$(pV)$-Diagramm

Rechts dargestellt sind die Kurven der Wertepaare $(V, p)$ für das im Zylinder eingeschlossene Arbeitsgas, dargestellt in einem Koordinatensystem mit dem Volumen $V$ als horizontaler und dem Druck $p$ als vertikaler Achse. Ein ideales Gas kann im Prinzip alle denkbaren Kombinationen $(V, p)$ annehmen. Aufgrund der allgemeinen Gasgleichung ist aber, wenn wir sowohl $V$ als auch $p$ festlegen, die Temperatur des Gases $T$ bereits bestimmt, die gilt nämlich immer:

$p \cdot V = N \cdot k_B \cdot T$

wo $N$ die Zahl der Moleküle im Gas und $k$ die Boltzmann-Konstante²⁷⁾ sind. Umgekehrt bestimmt sich, wenn wir außer dem Volumen $V$ noch die Temperatur $T$ festlegen²⁸⁾ der Druck nach:

$p=\frac{N \cdot k_B \cdot T}{V}$

So ergeben sich zu konstanten Temperaturen die Hyperbeln als Darstellung für die Isothermen. Eingezeichnet ist hier die Isotherme zur hohen Temperatur $T_h$ in rot und die zur niedrigen Temperatur $T_c$ in blau. Der „Kreisprozess“ im Diagramm wird beim 'Motor' rechtsherum durchlaufen. Ein Blick auf dieses Diagramm verdeutlicht den gesamten Stirling-Prozess, den wir oben in vier Teilprozessen ausführlich beschrieben haben.

_{Das $pV$-Diagramm des Stirling-Motors}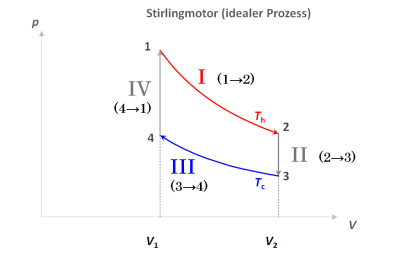

In den Lehrbüchern wird der Stirlingprozess oft anhand dieses $(p , V)$-Diagramms behandelt. Hier wird unmittelbar sichtbar, wie die Arbeitsdifferenz als Differenz der Flächen unter der oberen und der unteren Isotherme resultiert²⁹⁾. Die im Kreisprozess eingeschlossene Fläche charakterisiert die gesamte von der Maschine insgesamt abgegebene Arbeit.

Animation: idealisierter Stirling-Prozess

Hier ist die gesamte Animation, wie diese Maschine im Grundprinzip funktioniert: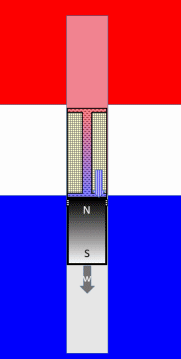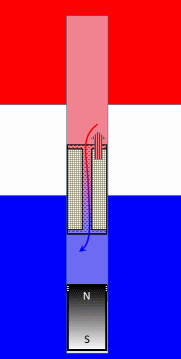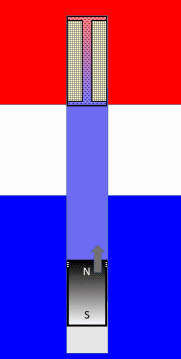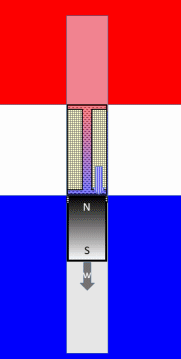
Das Arbeitsgas im Zylinder wird zwischen dem heißen (rot) und dem kalten (blau) Bereich hin- und hergeschoben. Das wird mit einem geregelt gesteuerten „Verdrängungskolben“ (hier hellgelb „Isolationsmaterial“) erreicht³⁰⁾. Das Gas kann mechanisch ungehindert durch den Strömungskanal im Verdrängungskolben durchtreten. Der Strömungskanal enthält ein Wärmespeichermedium („Regenerator“³¹⁾). Der schwarzweiße Arbeitskolben ³²⁾ sitzt dicht im Zylinder; bei seiner Verschiebung (gegen einen konstanten Umgebungsdruck) arbeitet das Gas. Als Arbeitsmaschine³³⁾ erfolgt die Expansion des Gases dann, wenn es sich im heißen Bereich $T_h$ befindet, weil da der Druck am höchsten ist und die vom Gas geleistete Arbeit am größten. Die Kompression zurück auf das kleinste Volumen erfolgt dann, wenn das Gas am kältesten ist $T_c$; dazu muss natürlich Arbeit aufgewendet werden, wegen des geringeren Druckes aber weniger³⁴⁾.

_{Stirling Prozess}

Stirlingmotor - Was er macht

Da wir den vollen Zyklus jetzt beschrieben haben, können wir alle vier Einzelprozesse in Ihrer Abfolge betrachten und zusammenfassen:

Beginnen wir aus Sicht des heißen Temperaturreservoirs $T_h$: Das wird nur vom Teilprozess I angezapft und ihm wird dabei die Wärme $Q_I$ entnommen:

$Q_I=C_{Maschine}\cdot T_h .$

Das ist die Energiebereitstellung, welche für den Betrieb des Motors erfolgen muss („Input“ für ein Energieflussbild).

Dagegen wird das kalte Temperaturreservoir ausschließlich im Schritt III mit Wärme beschickt:

$Q_{III}=-C_{Maschine}\cdot T_c .$

das ist aus Kraftwerkssicht Verlustwärme. Weil sie genau auf der „Umgebungstemperatur“ $T_c$ abgeführt wird, kann damit niemand mehr etwas anfangen; es ist aus praktischer Sicht vollkommen entwertete Energie³⁵⁾ ³⁶⁾.

Der Nutzen der Maschine ist die in der Gesamtbilanz über den Zyklus abgegebene Arbeit, die wir zu

$w_{tot}=w_I + w_{III}= C_{Maschine} (T_h - T_c)$

bestimmt haben. Das ist der nutzbare „Output“ und damit lässt sich sofort der Wirkungsgrad dieses Motors bestimmen $\eta=\frac{Output}{Input}$:

$\eta=\frac{w_{tot}}{Q_I}=\frac{C_{Maschine} (T_h - T_c)}{C_{Maschine}\cdot T_h}$

Die maschinenspezifischen Eigenschaften kürzen sich heraus, es bleibt

${\displaystyle \eta=\frac{T_h - T_c}{T_h}}$

Das ist eine wohlbekannte Größe, nämlich der sogenannte Carnot-Wirkungsgrad, der 1824 erstmals von Nicolas Léonard Sadi Carnot mit dem auch nach ihm benannten Carnot-Prozess bestimmt wurde. Wie wir in der Folge noch sehen werden, hat dieser Wirkungsgrad eine fundamentale physikalische Bedeutung, völlig unabhängig von der speziellen Art von Maschine, mit der die Energieumwandlungen durchgeführt werden.

Wir zeigen ein paar Bespiele für die mit idealen reversiblen Maschinen erreichbaren Carnot-Wirkungsgrade. Dort wird auch gleich die Exergie als der „wertvolle Teil“ eines Energiestroms eingeführt.

Zurück zum Kapitel 2. Hauptsatz

Weiter zum Kapitel Stirlingwärmepumpe

Zurück zur Kursübersicht "Bauphysik"

Anhang zu einem Einwand: ideale und praktische Maschine

Hier gibt es dann oft einen 'prinzipiell' klingenden Einwand: Diese Kombimaschine aus einem idealen Stirlingmotor und einer idealen Stirling-Wärmepumpe wäre dann ein echtes Perpetuum mobile: Eine Maschine, die ohne sonstige Änderungen in der Natur dauernd von selbst läuft - und „eine solche darf es doch gar nicht geben.“ Wir lösen dies als Scheinwiderspruch im Folgenden auf:

Zunächst einmal ist klar, dass auch diese ideale Kombimaschine keine freie Arbeit liefert. Sie läuft „nur“. Und weil selbst das Feststellen dieses 'Laufens' einen geringfügigen Energiebetrag erfordert, könnten wir, so es diese ideale Maschine ansonsten wirklich gäbe, diesen Zustand in der Praxis noch nicht einmal verifizieren.
Schon aus dem ersten Punkt wird klar, dass es die ideale Kombimaschine eben in der Praxis dann doch nicht gibt; sie ist nur eine theoretisches Konstruktion, freilch eine sehr hilfreiche. Geringfügige „Schmutzeffekte“ gibt es eben immer, z.B. dass es bei einer Temperaturdifferenz von „Null“ zwischen dem heißen Reservoir und dem heißen Prozessabschnitt unendlich lange dauern würde, bis dabei überhaupt Wärme übertragen wird. Andersherum: Damit in endlicher Zeit Wärme übertragen wird, wird es immer eine, im Grundsatz auch „extrem kleine“ Temperaturdifferenz an dieser Stelle geben müssen; und genau dieser Teilprozess ist dann wieder wirklich irreversibel, d.h. eine in der Praxis realisierte Maschine wird den Wirkungsgrad der idealen Kombimaschine nie exakt erreichen, sondern ein wenig darunter bleiben. Das kann wiederum extrem wenig sein, d.h., auch die praktische Maschine könnte dem idealen Kombiprozess sehr nahe kommen - nur, diesen eben nicht exakt erreichen.
Eine letzte Bemerkung aus der Anwendungspraxis dazu: Ob so ein Wirkungsgrad (z.B. des Stirlingmotors) im Einzelfall nun z.B. 48% tatsächlich erreicht oder doch nur 47,8% - das ist auch für die Praxis unbedeutend. Die heute tatsächlich vorliegenden Abstände zwischen dem ideal Möglichen und dem bisher Üblichen liegen eher bei Faktoren 1,5 bis 10. Die „2“ z.B. bei einem konkreten Kohlkraftwerk, die „10“ bei den Wärmeverlusten eines beheizten Gebäudes. Da gibt es somit einen enormen Spielraum - auch wenn „exakt ideal“ nicht erreichbar ist.</WRAP>

¹⁾

„Reservoir“ bedeutet, dass diese Wärme dort sofort wieder nachgeliefert wird; das kann in der Praxis so geschehen, dass ein geregelter Brenner genau die entnommene Wärme wieder bei genau der Temperatur $T_h$ erzeugt; so wird das z.B. in einem Kohlkraftwerk gemacht. Dadurch bleibt die Temperatur im Reservoir konstant - genau das definiert ein Temperatur-Reservoir

²⁾

c für cool = kühl

³⁾

In praktisch gebauten Kraftwerken ist das. z.B. die Atmosphäre und die 'Verlustwärme' genannte Wärmeabfuhr erfolgt z.B. mit einem Kühlturm. Bei Wärmekraftwerken mit hohen Leistungen ist auch diese Abwärmeleistung in aller Regel hoch, sie ist meist sogar höher als die gewonnenen mechanische Leistung. Das beeinträchtigt die Standortwahl solcher Kraftwerke (an der Küste, an einem Fluss, …) und kann sogar zum begrenzenden Problem für den Kraftwerksausbau werden. Wie wir hier sehen, ist das nicht eine Laune der Technik, sondern eine prinzipielle physikalische Eigenschaft solcher Wärmekraftmaschinen.

⁴⁾

Das geht, dazu muss allerdings Arbeit aufgewendet werden

⁵⁾

die wir zunächst speichern können

⁶⁾

Zu einem hier jetzt möglichen Einwand siehe den Anhang am Ende des Kapitels.

⁷⁾

in beliebig guter Näherung; natürlich nie 100% verlustfrei… aber im Grundsatz beliebig nahe dran, vgl. dazu auch "Einwand"

⁸⁾

'Heiß' ist da die Feuerung (die immer wieder viel Wärme liefern kann) und 'kalt' ist ein System der Umgebung, idealerweise Flusswasser, das immer wieder viel Wärme aufnehmen kann

⁹⁾

Den Druck im Arbeitszylinder bezeichnen wir hier wie üblich mit dem Formelzeichen $p$

¹⁰⁾

mit guter Näherung

¹¹⁾

einerseits weil das „Standardtechnik“ ist, die auf verschiedenste Weise leicht ergänzt und realisiert werden kann. Andererseits um die Darstellung hier nicht unnötig zu verkomplizieren

¹²⁾

iso = gleich; therm = hier: Temperatur; somit „isotherm“ = bei gleichbleibender Temperatur; Expansion = Ausdehnung

¹³⁾

sie kann z.B. magnetisch vom Kolben abgeholt werden

¹⁴⁾

in idealisierter Annahme

¹⁵⁾

Wir sehen schon, für den idealen Stirling-Prozess werden einige Idealisierungen angesetzt, die z.T. sogar in Konkurrenz zueinander stehen. Mit etwas Sorgfalt ist es aber durchaus auch in der Praxis möglich, so eine Maschine mit nur geringen Abweichungen vom Idealprozess zu bauen. Bis zu einem gewissen Punkt hilft „langsam laufen lassen“, weil dann Reibung und Strömungsturbulenzeffekte geringer sind und die Teile jeweils Zeit haben, sich thermisch an veränderte Bedingungen anzupassen. Werden die Zeiten aber „zu lang“, dann machen sich immer mehr Querwärmeströme (z.B. über die Zylinderwandung) bemerkbar, die ebenfalls das Idealverhalten empfindlich stören

¹⁶⁾

Das ist auch eine Idealisierung, weil es in er Realität natürlich eine gewisse Reibung gibt und der Kolben auch nicht ganz massefrei sein kann. Diese Verluste können aber klein gehalten werden, z.B. durch langsamen Lauf der Maschine

¹⁷⁾

Kraft in Bewegungsrichtung

¹⁸⁾

Die genaue Quantifizierung der 'Maschinenkonstante' $C_{Maschine}$ wird in Spalte drei dargestellt; sie setzt aber ein wenig Integralrechnung voraus.

¹⁹⁾

Es ist auch nicht 'so schwierig' wie es manchmal den Eindruck macht.

²⁰⁾

Zu der gibt es in Passipedia eine Herleitung: "die ideale Gasgleichung"

²¹⁾

Molekülzahl $N$, Boltzmann-Konstante $k_B$ und Temperatur $T_h$ sind auf dem gesamten Teilprozess konstant und können vor die Summe (das Integral) gezogen werden. Es verbleibt das Integral $\int \frac{dV}{V}$. Das hängt nur von den geometrischen Eigenschaften des Zylinders und der unteren und oberen Begrenzung der Kolbenbewegung ab, liefert somit einen Wert, der diese Maschine kennzeichnet. Mit der Mathematik Vertraute werden erkennen, dass dieses Integral den Logarithmus liefert: Damit ist hier sogar eine geschlossene Lösung möglich. Es würde aber auch ausreichen, die Summation näherungsweise über kleine Schrittchen numerisch durchzuführen.

²²⁾

Herkunft: griechisch ἴσως → „gleich“ und χῶρος → „Raum“

²³⁾

In der Praxis geht das natürlich nicht „perfekt“, zumal eine gewisse Temperaturdifferenz gebraucht wird, damit das Gas die Wärme überhaupt an das Regenerator-Material abgeben kann. Wieder kann das aber beliebig genau angenähert werden, auch hier z.B. dadurch, dass der Teilprozess ganz langsam abläuft.

²⁴⁾

Wärmeaufnahmefähigkeit des einzelnen Moleküls

²⁵⁾

oder zyklischen Prozess

²⁶⁾

energietechnisch ist das ein Wärmeverlust, weil wir die Wärme aus dem unteren Reservoir nicht mehr nutzen

²⁷⁾

$k=1,38064852 \cdot 10^{-23} m^2\, kg\, s^{-2} K^{-1}$

²⁸⁾

das gilt z.B. für die oben beschriebenen 'isothermen Teilprozesse„

²⁹⁾

Die Flächen unter Kurven im $(p , V)$-Diagramm sind nämlich die vom Gas an die Umgebung geleistete Arbeit, weil $p$d$V$ die Arbeit auf einem kleinen Teilstück ist

³⁰⁾

Weil der Druck im Gas räumlich überall der gleiche ist und hier eine idealisiert reibungsfreie Verschiebung sowie vernachlässigbar kleine Masse angenommen wird, braucht es für die Verschiebung des Verdrängungskolbens (so gut wie) keine Arbeit.

³¹⁾

Regenerationswärmeübertrager

³²⁾

N…S als Magnet dargestellt, wir koppeln die Arbeit magnetisch aus

³³⁾

hier dargestellt

³⁴⁾

die hier aufzuwendende Arbeit muss von der Maschine während des Expansionsprozesses gewonnen und erstmal mechanisch zwischengespeichert werden, z.B. mit einem Schwungrad

³⁵⁾

dafür werden wir in Kürze die Größe „Anergie“ einführen

³⁶⁾

Hier gibt es einen weit verbreiteten Irrtum: Weil es sich bei diesem Wärmestrom praktisch um Wärme bei Umgebungstemperatur handelt, kann mit dieser tatsächlich nichts „Sinnvolles“ mehr angestellt werden, auch dann nicht, wenn es sich um große Wärmemengen handelt. Die Unkenntnis dieser Zusammenhänge führt auf die leider recht oft zu findende Wunschvorstellung von „Energie im Überfluss“. Soll der Energiestrom noch irgendwie genutzt werden, so muss die Maschine bei einer gegenüber der Umgebung etwas höheren Temperatur $T_c+\Delta T$ betrieben werden. $\Delta T$ muss hoch genug sein, um z.B. den Vorlauf eines Fernwärmenetzes erwärmen zu können; andererseits nimmt der Wirkungsgrad bei der Erzeugung der Arbeit durch die Maschine dann ab. Wie sich das im konkreten Fall „aufwiegt“ und welche Betriebsweise letztlich die günstigere ist kann im konkreten Fall durchgerechnet werden.