Inhaltsverzeichnis
U-Werte von Mehrfachverglasungen quantitativ
Ein einzelner Scheibenzwischenraum
Zwischen der ebenen Oberfläche einer Gasscheibe auf der linken Seite und der ebenen Oberfläche der folgenden Glasscheibe auf der rechten Seite befindet sich ein gasgefüllter Scheibenzwischenraum mit konstanter Dicke d. Zwischen den beiden Oberflächen wird Wärme übertragen durch alle drei prinzipiell möglichen Mechanismen: Wärmeleitung, Wärmekonvektion und Wärmestrahlung. Die behandeln wir nun im Einzelnen.
Konvektiver Wärmeübergang im Spalt ${\Lambda_{cc}}$
Genau diesen Fall von kombinierter Wärmeleitung und Konvektion haben wir bereits im Abschnitt "freie Konvektion im Spalt" behandelt, wir hatten als gute Näherung das Ergebnis
${\displaystyle \Lambda_{cc} = \frac{\lambda}{\text{Min}(d, d_{Grenz})}} $
für den Wärmedurchlasskoeffizienten der Gasschicht zwischen den beiden Oberflächen erhalten.
Strahlungswärmeübergang im Spalt ${\Lambda_{rad}}$
Auch diesen Fall der Wärmeübertragung durch Wärmestrahlung zwischen zwei Oberflächen haben wir bereits im Abschnitt "Wärmestrahlung" behandelt, wir hatten dort als Ergebnis erhalten
${\displaystyle \Lambda_{rad}=\frac{\sigma (T_1^2 + T_2^2)(T_1 + T_2)}{\frac{1}{\varepsilon_1}+\frac{1}{\varepsilon_2}-1} }$ .
Dabei sind $\varepsilon_1$ die Emissionsgrade der Oberfläche der linken Seite und $\varepsilon_2$ der rechten Seite. Handelt es sich um normales Floatglas mit $\varepsilon = 0,84$ ohne Beschichtung, so ergeben sich die Werte aus folgender Tabelle bei einem Scheibenabstand von 15mm.
| Beitrag zum Wärmetransport | Formelzeichen | Berechnung | Wert des Wärmedurch- lasskoeffizienten |
|---|---|---|---|
| (Luftfüllung, Oberflächen unbeschichtet) | W/(m²K) | ||
| konvektiv (Luft) | $\Lambda_{cc}$ | $\frac{\lambda}{\text{Min}(d, d_{Grenz})}$ | 1,67 |
| Strahlung (Glas, unbeschichtet) | $\Lambda_{rad}$ | $\frac{\sigma (T_1^2 + T_2^2)(T_1 + T_2)}{\frac{1}{\varepsilon_1}+\frac{1}{\varepsilon_2}-1}$ | 3,78 |
| Summe Wärmedurchg. | $\Lambda_{cc} + \Lambda_{rad}$ | 5,45 | |
| Beitrag zum Wärmetransport | Formelzeichen | Berechnung | Wert des Wärmedurch- lasskoeffizienten |
|---|---|---|---|
| (Argonfüllung, Oberflächen unbeschichtet) | W/(m²K) | ||
| konvektiv (Ar) | $\Lambda_{cc}$ | $\frac{\lambda}{\text{Min}(d, d_{Grenz})}$ | 1,12 |
| Strahlung (Glas, unbeschichtet) | $\Lambda_{rad}$ | $\frac{\sigma (T_1^2 + T_2^2)(T_1 + T_2)}{\frac{1}{\varepsilon_1}+\frac{1}{\varepsilon_2}-1}$ | 3,78 |
| Summe Wärmedurchgang | $\Lambda_{cc} + \Lambda_{rad}$ | 4,90 | |
| Beitrag zum Wärmetransport | Formelzeichen | Berechnung | Wert des Wärmedurch- lasskoeffizienten |
|---|---|---|---|
| (Luftfüllung, eine low-e-Schicht) | W/(m²K) | ||
| konvektiv (Luft) | $\Lambda_{cc}$ | $\frac{\lambda}{\text{Min}(d, d_{Grenz})}$ | 1,67 |
| Strahlung (Glas, low-e-beschichtet) | $\Lambda_{rad}$ | $\frac{\sigma (T_1^2 + T_2^2)(T_1 + T_2)}{\frac{1}{\varepsilon_1}+\frac{1}{\varepsilon_2}-1}$ | 0,258 |
| Summe Wärmedurchgang | $\Lambda_{cc} + \Lambda_{rad}$ | 1,925 | |
| Beitrag zum Wärmetransport | Formelzeichen | Berechnung | Wert des Wärmedurch- lasskoeffizienten |
|---|---|---|---|
| (Argonfüllung, eine low-e-Schicht) | W/(m²K) | ||
| konvektiv (Ar) | $\Lambda_{cc}$ | $\frac{\lambda}{\text{Min}(d, d_{Grenz})}$ | 1,12 |
| Strahlung (Glas, low-e-beschichtet) | $\Lambda_{rad}$ | $\frac{\sigma (T_1^2 + T_2^2)(T_1 + T_2)}{\frac{1}{\varepsilon_1}+\frac{1}{\varepsilon_2}-1}$ | 0,258 |
| Summe Wärmedurchgang | $\Lambda_{cc} + \Lambda_{rad}$ | 1,378 | |
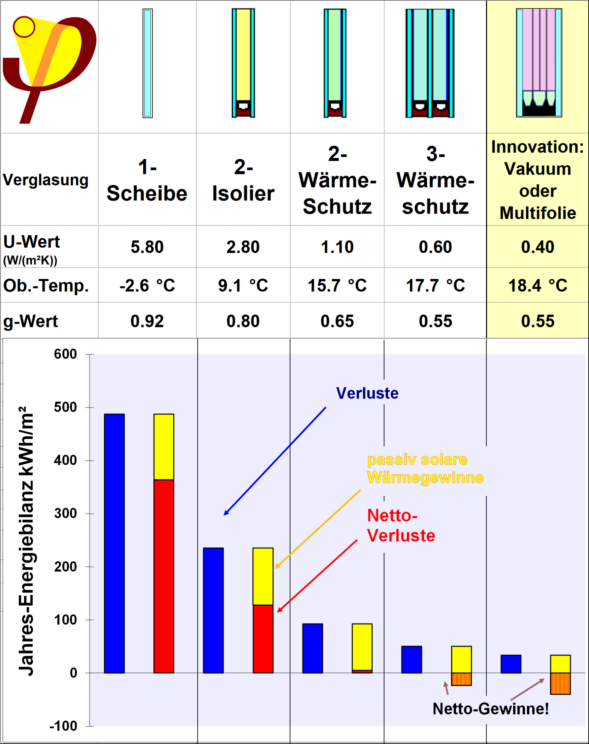
Durch die Wärmestrahlungs-reflektierende Beschichtung wird der Wärmetransport durch die Strahlung so stark reduziert, dass nun doch die Wärmeleitung im Füllgas den überwiegenden Teil der Übertragung übernimmt. Nun lohnt es sich auch, statt der Luft dort das besser isolierende Argon zu verwenden (4. Tabelle). Insgesamt wird der Wärmtransport zwischen den beiden Oberflächen so von 5,45 W/(mK) auf nur noch 1,38 W/(m²K) reduziert - das ist eine Verbesserung um fast einen Faktor 4.
Dass Metallschichten Wärmestrahlung reflektieren wussten die Physiker eigentlich schon über 150 Jahre; das auf Fensterverglasungen anzuwenden, darauf war allerdings zunächst niemand gekommen. Denn: Metallschichten wirken wie Spiegel, das ist wohlbekannt, und es gilt für das gesamte Spektrum der elektromagnetischen Strahlung. 'Spiegel' waren schon immer so aufgebaut. Aber natürlich schien das für eine Fenster-Verglasung kontraproduktiv, denn schließlich wollen wir uns in dieser nicht spiegeln, sondern wir wollen hindurchschauen. Dies war nun der entscheidenden Durchbruch, zu erkennen, dass sehr dünne Metallschichten für das sichtbare Licht durchlässig werden, das langwelligere mittlere Infrarot (das ist die Wärmestrahlung) aber immer noch sehr gut reflektieren: Wir sprechen hier von einer selektiv wirksamen Beschichtung. Nach der klassischen Physik würden wir von Metallschichten jeder Dicke Reflexion über das gesamte Spektrum erwarten; nach der Quantenmechanik allerdings können kurzwelligere Photonen wie die des sichtbaren Lichtes den Potentialwall durch die freien Elektronen in der hauchdünnen Metallschicht durchtunneln. Low-e-Wärmeschutz-Verglasungen sind damit makroskopisch wirksam angewandte Quantenmechanik; heute kann somit jeder Nutzer eines Gebäudes mit modernen Wärmschutzverglasungen die Außenwelt durch die Verglasung nur infolge des quantenmechanischen Tunneleffektes sehen. Dass diese Anwendung möglich ist, erspart uns heute rund 3/4 der Wärmeverluste durch moderne Verglasungen. Dieser offensichtliche technologische Fortschritt ist ein gutes Beispiel für die unmittelbare Anwendung von Forschungsergebnissen aus der modernen Physik in die Praxis. Dieser entscheidende Fortschritt wurde übrigens weitgehend unabhängig voneinander von zwei Kollegen, Prof. Arthur Roesenfeld in Californien und Prof. Hans Joachim Gläser in Deutschland ermöglicht.
Der Aufwand für diese Beschichtungen ist i.Ü. nicht besonders groß; eine hauchdünne Silberschicht wird in einer evakuierten Kammer aufgesputtert. Das kostet in der industriellen Produktion nur wenige Euro je Quadratmeter. Die dadurch erzielte Heizwärmeeinsparung beträgt aber weit über 10 € je Quadratmeter in jedem Jahr - diese Verbesserung der Energieeffizienz ist somit sehr wirtschaftlich. Auch das Füllen der Gaszwischenräume mit dem Edelgas Argon statt mit Luft kostet maximal wenige Euro je Quadratmeter. Beides fällt bei den Gesamtkosten eines Fensters kaum ins Gewicht1) .
Zusammensetzen mehrerer Scheiben zu Mehrscheiben-Wärmeschutzverglasung
Nachdem wir die Wärmedurchlasskoeffizienten und damit die Wärmedurchlasswiderstände der gasgefüllten Scheibenzwischenräume inkl. der Wärmestrahlung im letzten Abschnitt komplett berechnen konnten, lassen sich jetzt Mehrscheibenverglasungen durch einfaches Aufsummieren alle Wärmedurchlasswiderstände bestimmen:
$\displaystyle{ R_{ges} = R_{si} + \frac{s_1}{\lambda_g} + \frac{1}{\Lambda_{rad,1}+\Lambda_{cc,1}} + \frac{s_2}{\lambda_g} + \frac{1}{\Lambda_{rad,2}+\Lambda_{cc,2}} + \frac{s_3}{\lambda_g} + ... + R_{se} } $
Dabei sind $s_j$ die Dicken der Glasscheiben und $\lambda_g$ die Wärmeleitfähigkeit des verwendeten Glases und die $\Lambda$-Werte die jeweils ermittelten konvektiven und radiativen Wärmedurchlasskoeffizienten der Gaszwischenräume.
| innerer Wärme- überg. innen | Glas- scheibe innen | Zwi- schen- raum I | Glas- scheibe | evtl. Zwi. schen- raum II | Glas- scheibe | evtl. Zwi.- raum III | Glas- scheibe | äußerer Wärme- überg. | Rges | U-Wert | % | Jahreskost- einspar. gegen 2ISO Euro/(m²a) | Barwert derselben Euro/m² |
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m²K/W | m²K/W | m²K/W | m²K/W | m²K/W | m²K/W | m²K/W | m²K/W | m²K/W | m²K/W | W/(m²K) | €/a | € | ||
| Einfach-Vgl. | 0,13 | 0,004 | 0,040 | 0,174 | 5,75 | 100% | ||||||||
| Zweisch.-Isolierglas /Luft /ohne low-e | 0,13 | 0,004 | 0,184 | 0,004 | 0,040 | 0,362 | 2,77 | 48% | 0,00 | 0,00 | ||||
| Dreisch.-Isolierglas /Luft /ohne low-e | 0,13 | 0,004 | 0,184 | 0,004 | 0,184 | 0,004 | 0,040 | 0,549 | 1,82 | 32% | 7,48 | 187,02 | ||
| Zweisch.-Wschutzglas /Argon 16mm /low-e | 0,13 | 0,004 | 0,764 | 0,004 | 0,040 | 0,942 | 1,06 | 18% | 13,50 | 337,36 | ||||
| Dreisch.-Wschutzglas /Argon 2*16mm /2*low-e | 0,13 | 0,004 | 0,764 | 0,004 | 0,764 | 0,004 | 0,040 | 1,711 | 0,58 | 10% | 17,27 | 431,73 | ||
| Viersch.-Wschutzglas /Argon 3*16mm /3*low-e | 0,13 | 0,004 | 0,764 | 0,004 | 0,764 | 0,004 | 0,764 | 0,004 | 0,040 | 2,479 | 0,40 | 7% | 18,71 | 467,60 |
Für die Tabelle haben wir $\varepsilon = 0,05$ angesetzt, entsprechend einer hochentwickelten modernen Beschichtung. Die Tabelle geht dabei jeweils von 100% Füllgrad mit dem angegebenen Gas aus. In der Praxis werden diese Füllgrade nicht erreicht, realistisch Werte liegen zwischen 80% und 95%. Dadurch werden die U-Werte etwas höher.
Die hier beschriebenen technologischen Innovationen haben es über die vergangenen 50 Jahre ermöglicht, die Qualitäten von Fensterverglasungen um Faktoren zu verbessern - dabei sind diese aber noch nicht einmal bedeutend im Preis gestiegen.
Zurück zum Kapitel Übersicht Verglasung 🌡️
Weiter zum Kapitel zur solaren Einstrahlung 🌡️
Zurück zum Grundkurs Bauphysik Wärme - Übersicht 🌡️