In der Bauphysik sind in aller Regel nur die gesamten (integralen) Energieströme durch Wärmestrahlung relevant, für den idealen Strahler (schwarzen Körper) sind die Werte der Abstrahlung von einer Fläche nach dem Stefan-Boltzmannschen Gesetz (Index e für Emission) gegeben:

${\displaystyle \dot{q_{e}}= \sigma T^4 }$

Reale Objekte haben aber keinen 100% Emissionsgrad; in aller Regel lassen sie sich aber für einen Wellenlängenbereich, wie z.B. den der thermischen Strahlung in der Umgebung der Raumtemperatur (also ca. 0 bis 40 °C) durch einen 'grauen Körper' mit konstantem Emissionsgrad $\varepsilon$ < 1 annähern. Sie emittieren dann das $\varepsilon$-Fache des o.g. Wertes. Stehen sich zwei Körper mit verschiedener Temperatur gegenüber, so senden beide Wärmestrahlung aus und absorbieren¹⁰⁾ die des anderen (Beispiele: innere und äußere Scheibe einer Zweischeibenverglasung, Erdboden-Wolkendecke bzw. Erdboden-klarer Nachthimmel). In diesem Fall spricht man von Strahlungsaustausch. Als einfaches Beispiel werden zwei unendlich ausgedehnte parallele ebene Körper in einem bestimmten Abstand voneinander betrachtet. Der Nettostrahlungsfluss $\dot{q}_{rad} $ lässt sich wie folgt aus dem Strahlungsstrom $\dot{q}_1$ von 1 nach 2 und von $\dot{q}_2$ in die andere Richtung bestimmen

$\dot{q}_{rad}= \dot{q}_1 - \dot{q}_2 ~,$

wobei die Wärmeströme sich aus der primären thermischen Abstrahlung („Selbststrahler“) und der reflektierten Strahlung zusammensetzt:

$\dot{q}_{1}=\dot{q}_{e,1} - \varrho_1 \dot{q}_2 ~,$
$\dot{q}_{2}=\dot{q}_{e,2} - \varrho_2 \dot{q}_1 ~,$

Die beiden letzten Gleichungen können nach den gerichteten Gesamtwärmeströmen aufgelöst werden¹¹⁾, für die jeweilige Strahlungserzeugung $\dot{q}_e$ setzen wir dann die erste Gleichung multipliziert mit dem jeweiligen Emissionsgrad ein und bestimmen dann deren Differenzen. Dabei nehmen wir an, dass die beiden Oberflächen opak sind, d.h. es ist $\varrho_j = 1 - \varepsilon_j .$ Das ergibt

${ \displaystyle \dot{q}_{rad}= \frac{\sigma}{\frac{1}{\varepsilon_1}+\frac{1}{\varepsilon_2}-1} \left( T_1^4 - T_2^4 \right) ~},$

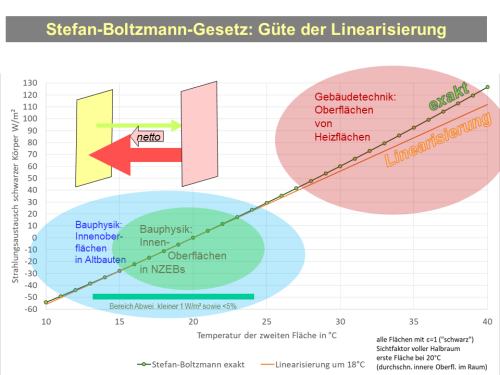
Damit lässt sich (weitgehend exakt) der netto-Wärmestrom durch Strahlung zwischen zwei Fensterscheiben aber auch in guter Näherung der Netto-Strahlungsaustausch zwischen Fußboden und Decke¹²⁾ bestimmen. Das hier jeweils die Potenz $T^4$ bestimmt werden muss, ist bei der heutigen Verfügbarkeit von Taschenrechner und Computer eigentlich kein Hindernis. Es ist aber auch zulässig (und üblich) eine lineare Näherung für die Abhängigkeit von der Temperaturdifferenz zu verwenden, weil die absoluten Temperaturen im Bereich der Bauphysik sich doch alle in einem recht engen Bereich (dem Komfortbereich!) bewegen: $15 °C < \vartheta < 28 °C$. Dazu wenden wir auf die Differenz der $T^4$-Terme einfach zweimal den dritten binomischen Lehrsatz an:

$T_1^4 - T_2^4 = (T_1^2 + T_2^2) (T_1^2 - T_2^2)= (T_1^2 + T_2^2) (T_1 + T_2)(T_1 - T_2)$

Da steht jetzt vor allem die Temperaturdifferenz $(T_1 - T_2)=(\vartheta_1 - \vartheta_2)$ drin. Die beiden Summenterme ziehen wir mit dem Netto-Emissionsgrad zusammen zu

${\displaystyle \dot{q}_{rad}=\frac{\sigma (T_1^2 + T_2^2)(T_1 + T_2)}{\frac{1}{\varepsilon_1}+\frac{1}{\varepsilon_2}-1} \left( \vartheta_1 - \vartheta_2 \right) ~,}$

und mit dem „Strahlungsaustausch-Wärmeübergang“ $h_{rad}$

${\displaystyle h_{rad}=\frac{\sigma (T_1^2 + T_2^2)(T_1 + T_2)}{\frac{1}{\varepsilon_1}+\frac{1}{\varepsilon_2}-1} }$

ergibt sich dann

${\displaystyle \dot{q}_{rad}= h_{rad} (\vartheta_1 - \vartheta_2) } $

Damit können wir den Strahlungswärmeaustausch in guter Näherung wie einen Wärmeübergang schreiben, der allerdings von einer Oberfläche zur anderen stattfindet. Für Temperaturen in der Umgebung von 18 °C (mittlere Temperaturen von Raum und Innenoberflächen von Außenbauteilen) kann noch eine Näherung für den Faktor

${\displaystyle h_{rad}=\varepsilon_n \sigma (T_1^2 + T_2^2)(T_1 + T_2) \approx \varepsilon_n 5,6 }$ W/(m²K)

angegeben werden. Dabei haben wir den Netto-Emissionsfaktor durch $\varepsilon_n=\frac{1}{1/\varepsilon_1 + 1/\varepsilon_2 -1}$ abgekürzt. Die Strahlungswärmeübergänge bei raumüblichen Emissionsgraden von um 93% liegen damit so in etwa zwischen 4,8 und 5,4 W/(m²K) und sind damit DEUTLICH höher als die konvektiven Wärmeübergänge.

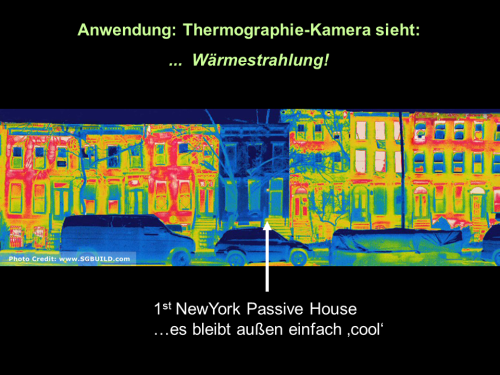
Der Wärmeaustausch im Raum findet somit zu einem sehr großen Teil über die Wärmestrahlung statt und gar nicht, wie in der naiven Vorstellung, über die Luft.

Das hat weitreichende praktische Konsequenzen: Das naive thermische Modell, dass Wärme im Raum über die Luft ausgetauscht wird, teilen leider auch noch viele 'Fach'-Leute. Der Wärmestrahlungsaustausch ist viel bedeutender! Der transportiert die Wärme auch direkt z.B. vom Heizkörper an die Außenbauteil-Innenoberfläche - oder vom beheizten Fußboden an die Dach-Innenoberfläche. Effekte, die zumindest für einen Teil der oft beobachteten höheren Energieverbrauchswerte¹³⁾ von Flächenheizungen beiträgt; nun ist dieser Effekt auch nicht so groß, dass die gewollten Einsparbeiträge durch größere Heizflächen dadurch ganz aufgehoben würden(Strahlungsklima, niedrigere Vorlauftemperaturen und daher Leitungsverluste, insbesondere aber bessere Arbeitszahlen von Wärmepumpen). Allerdings: Wenn ich einen Raum nur mal schnell und dann für kurze Zeit (< 1,5 h) in der Temperatur anheben will - dann geht das am effizientesten durch einen Lufterwärmer. Einmal wird die Luft wg. der geringen Wärmekapazität schnell warm; zum anderen überträgt sie innerhalb von 1,5 h keine gigantischen Wärmemengen an die Raumumfassungsflächen, so dass deren Temperaturen nicht so rasch ansteigen. Dadurch fällt die Temperatur dann auch nach dem Abschalten schnell wieder ab; das ist also ein „guter Trick“ um z.B. ein kleines Bad mal eben schnell und mit vertretbaren Kosten hochzuheizen.

Wie gut ist so eine Näherung? Im Bereich der innerhalb der Gebäude relevanten Wärmeaustauschvorgänge überraschend gut. Wenn konventionelle Heizkörper oder andere heiße Objekte mit ins Spiel kommen, rechnet man für die besser mit einem höheren Faktor. Es kann auch immer „exakt“ mit dem $T^4$-Gesetz gerechnet werden. Bedenke aber: Andere Größen, wie der konvektive Wärmeübergang, sind weit weniger genau bekannt (NZEB = nearly zero energy building, Fast-Null-Energie-Haus).

Die Praxis: Das Haus in der Mitte ist NICHT unbeheizt, es ist komfortabel warm. Aber durch die sehr gut wärmegedämmten Außenbauteile verliert es kaum Wärme, dadurch gleicht sich die Außenoberflächentemperatur der Umgebung an und nur wenig Wärmestrahlung wird emittiert. New York's '1st passivehouse' erscheint im Infrarotbild „cool“. Es handelt sich um eine Renovierung, diese Ergebnisse sind daher auch bei Bestands-Gebäuden erreichbar.

Was bedeutet das nun für die Temperaturen in Aufenthaltsräumen? Für einen Raum in Passivhaus-Qualität¹⁴⁾,heißt es zunächst, dass die Temperaturen im annähernd eingestellten Gleichgewicht kaum Unterschiede an verschiedenen Orten aufweisen. Eben weil der Strahlungsaustausch zwischen den Umfassungsflächen so groß, andererseits aber der Wärmeverlust durch Außenbauteile so gering ist, kann es nicht zu nennenswerten Unterschieden der stark miteinander durch Strahlung gekoppelten Oberflächentemperaturen kommen.

Beispiel: Eine Außenwand mit U-Wert 0,12 W/(m²K) überträgt bei einem Temperaturunterschied von 20 K einen Wärmestrom von 2,4 W/m² nach außen. Selbst im Winter ist also der Wärmeverlust nach außen nur halb so groß, wie es allein der Strahlungswärmeaustausch im Inneren des Raumes bei 1K Temperaturdifferenz ist. Die Oberflächentemperatur der Außenwand kann also nur eine maximal 0,5K geringere Temperatur als die übrigen Raum-Umfassungsflächen aufweisen. Zumindest bei stationären Bedingungen ist das der Fall - und die liegen im normalen Winterbetrieb eines Passivhauses mit guter Näherung vor¹⁵⁾.

Was ist das überhaupt, die Raumtemperatur? Auch die meisten Thermometer erfassen zu einem großen Anteil die Strahlungstemperatur der Umfassungsflächen und anderen Gegenstände. Nur ein Anteil des Messwerts ist auf die konvektive Kopplung an die Raumluft bestimmt. Es ergibt sich so ein gewichteter Mittelwert aus beiden Größen, die genauen Anteile hängen von der Bauart des Thermometers ab. Für übliche, an der Wand montierte Raumtemperatursensoren in Gehäusen sind ¾ (Strahlung) zu ¼ (konvektiv) eine realistische Größenordnung. Für Passivhäuser und EnerPHit Sanierungen ist das wiederum eher ein 'akademisches Problem', da sich bei diesen Luft- und Strahlungstemperaturen sich ohnehin kaum unterscheiden.

Zurück zur Übersicht Wärmestrahlung 🌡️

Zurück zum Grundkurs Bauphysik Wärme - Übersicht 🌡️