Inhaltsverzeichnis
Grundprinzip der Wärmebrückenberechnung 🌡️
Für die Berechnung der Wärmebrücken gilt es zunächst die entsprechenden Bauteilanschlüsse für eine Wärmestrom-Software zu modellieren. Neben der Geometrie müssen die einzelnen Wärmeleitfähigkeiten der Materialen angegeben werden. Des weiteren sind Randbedingungen für Temperaturen und Wärmeübergangswiderstände zu wählen. Die maßgebende Norm für Berechnung von Wärmebrücken im Bauwesen ist die DIN EN ISO 10211. Die Berechnungen des $\Psi$-Wertes und die Ermittlung der minimalen raumseitigen Oberflächentemperatur können am selben Modell vorgenommen werden, allerdings sind jeweils andere Randbedingungen zu wählen, wie nachfolgend gezeigt wird.
Ermittlung der Wärmedurchgangskoeffizienten
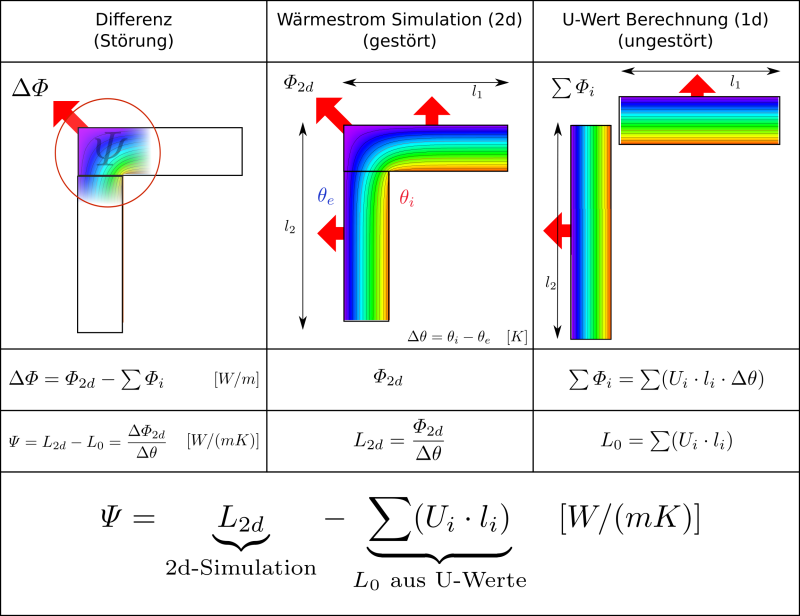
In der unteren Abbildung ist das Prinzip zur Berechnung des längenbezogenen Wärmedurchgangskoeffizienten dargestellt. Der $\Psi$-Wert stellt die Differenz zwischen dem thermisch gestörten und dem für die Bilanzierung angenommenen ungestörten Bauteil dar. Durch die Wärmestromsimulation wird zuerst der Wärmestrom bzw. der Leitwert $L_{2d}$ bestimmt. Um den $\Psi$-Wert zu bestimmen, wird nun der Leitwert des ungestörten Bauteils $L_{0}$ abgezogen. Wichtig ist, dass der einmal gewählte Längenbezug durchgängig eingehalten wird. Wird z.B. im Rahmen einer detaillierten dynamischen Simulation mit Innenmaßen gearbeitet, so müssen auch innenmaßbezogene $\Psi$-Werte verwendet werden. In der Praxis wird jedoch häufiger mit Außenmaßen gearbeitet, da diese einfacher aus Plänen und Aufmaß zu entnehmen sind. Im PHPP wird daher durchgehend mit dem Außenmaß gearbeitet. Wenn nicht ausdrücklich anders erwähnt, sind die Angaben hier auch immer konsequent auf die Außenmaße bezogen.
Randbedingungen / Übergangswiderstände
Da die Leitwerte unabhängig von den angesetzten Temperaturrandbedingungen sind, ist prinzipiell gleichgültig, welche Temperaturen für Innen bzw. für Außen angesetzt werden, solange es zu einem Temperaturgefälle durch das Bauteil kommt. Praktischerweise werden die gleichen Temperaturen verwendet, wie sie auch zur Ermittlung der minimalen Oberflächentemperatur angesetzt werden. Wichtiger sind die zu verwendenden Wärmeübergangswiderstände. Sie sind ein Maß für den Wärmeaustausch des Bauteils mit der Umgebung. In ihnen wird der Einfluss von Strahlungsaustausch, Wärmeleitung und Konvektion zusammengefasst. Deshalb sind sie unter anderem von der Beschaffenheit der Oberflächen (Rauigkeit, Farbe und Belüftung) und von der Richtung des maßgebenden Wärmestroms durch das Bauteil abhängig. Unterschieden wird zwischen $R_{si}$ für Innen und $R_{se}$ für Außen.
| Wärmeübergangswiderstand (m²·K)/W | Richtung des Wärmestroms | ||
|---|---|---|---|
| Aufwärts | Horizontal | Abwärts | |
| $R_{si}$ | 0,10 | 0,13 | 0,17 |
| $R_{se}$ | 0,04 | 0,04 | 0,04 |
Ermittlung der minimalen Oberflächentemperatur und des f-Faktors
Die Vorgehensweise zur Bestimmung der Oberflächentemperaturen ist ähnlich und kann in der Regel am gleichen Modell wie zur Berechnung des $\Psi$-Wertes erfolgen. Allerdings wird für den Innenraum ein erhöhter Übergangswiderstand $R_{si}$ angesetzt. Der Grund dafür ist, dass Schränke, Wandbehänge, Vorhänge und Ähnliches lokal die Konvektion und den Strahlungsaustausch an Ecken, Kanten und Wänden verringern, was letztendlich zu niedrigeren Oberflächentemperaturen führt. Um auf der sicheren Seite zu sein, wird von daher der erhöhte Übergangswiderstand von $R_{si}$ = 0,25 (m²·K)/W für den gesamten Innenraum verwendet (DIN 4108-2, Kapitel 6.3). Noch höhere Übergangswiderstände werden im Fachbericht 4108-8 empfohlen:
- $R_{si,äq}$ = 0,50 (m²·K)/W für Bereiche hinter freistehenden Schränken
- $R_{si,äq}$ = 1,00 (m²·K)/W für Bereiche hinter Einbauschränken
Temperatur-Randbedingungen
Da bei stationären Simulationen zeitliche Änderungen der Temperaturen und die Wärmekapazität der Materialien nicht berücksichtigt werden, müssen feste Temperaturrandbedingungen angesetzt werden, was letztendlich zu einem statischen Temperaturfeld im Bauteil führt. Dort lässt sich anschließend die minimale Oberflächentemperatur ablesen, die sich jedoch nur auf die jeweilige Temperaturdifferenz zwischen der angesetzten Innentemperatur und der Außentemperatur bezieht. In der Norm DIN 4108-2 (Kapitel 6.3) werden folgende Temperaturrandbedingungen angegeben:
- $\theta_i$ = 20 °C für die Innenlufttemperatur
- $\theta_e$ = −5 °C für die Außenlufttemperatur
Das Passivhaus Institut verwendet im Rahmen der Komponentenzertifizierung folgende Temperatur-Randbedingungen:
- $\theta_i$ = 20 °C für die Innenlufttemperatur
- $\theta_e$ = −10 °C für die Außenlufttemperatur
Es ist schnell klar, dass die so ermittelten minimalen Oberflächentemperaturen keine relevante Aussagekraft besitzen. Die oben genannten Temperaturrandbedingungen sind bestenfalls grobe Abschätzungen und können realistische Temperaturdifferenzen nicht wirklich darstellen. Die Unsicherheiten hinsichtlich der vom Klima abhängigen Außenbedingungen und den tatsächlichen Temperaturen im Innenraum sind zu groß. Wird auf dynamische Simulationen verzichtet, so kann die Problematik zumindest teilweise umgangen werden und zwar mit Hilfe des dimensionslosen Temperaturfaktor $f_{Rsi}$ nach DIN EN ISO 10211 (Kapitel 11).
\begin{align}
&f_{Rsi}(x,y,z)=\dfrac{\theta_{min}(x,y,z)-\theta_e}{(\theta_i-\theta_e)} \qquad \text{bzw. } \qquad f_{Rsi}(x,y)=\dfrac{\theta_{min}(x,y)-\theta_e}{(\theta_i-\theta_e)}\\\\
Mit\qquad&\\
f_{Rsi}\qquad&\text{der Temperaturfaktor am Ort $(x,y,z)$ bzw. $(x,y)$}\\
\theta_{min}\qquad&\text{die minimale Oberlächentemperatur am Ort $(x,y,z)$ bzw. $(x,y)$}\\
\theta_i\qquad&\text{die Innenlufttemperatur}\\
\theta_e\qquad&\text{die Außenlufttemperatur}
\end{align}
Der nach dieser Gleichung ermittelte Faktor ermöglicht es nun, die minimale Oberflächentemperatur an der entsprechenden Stelle für beliebige Temperaturdifferenzen zu berechnen, ohne das weitere Wärmestromsimulationen nötig sind. Mit Hilfe des $f_{Rsi}$-Faktors sind Rückschlüsse auf möglichen Kondenswasserausfall und Schimmelpilzwachstum möglich.
Beispiel einer Wärmebrückenberechnung
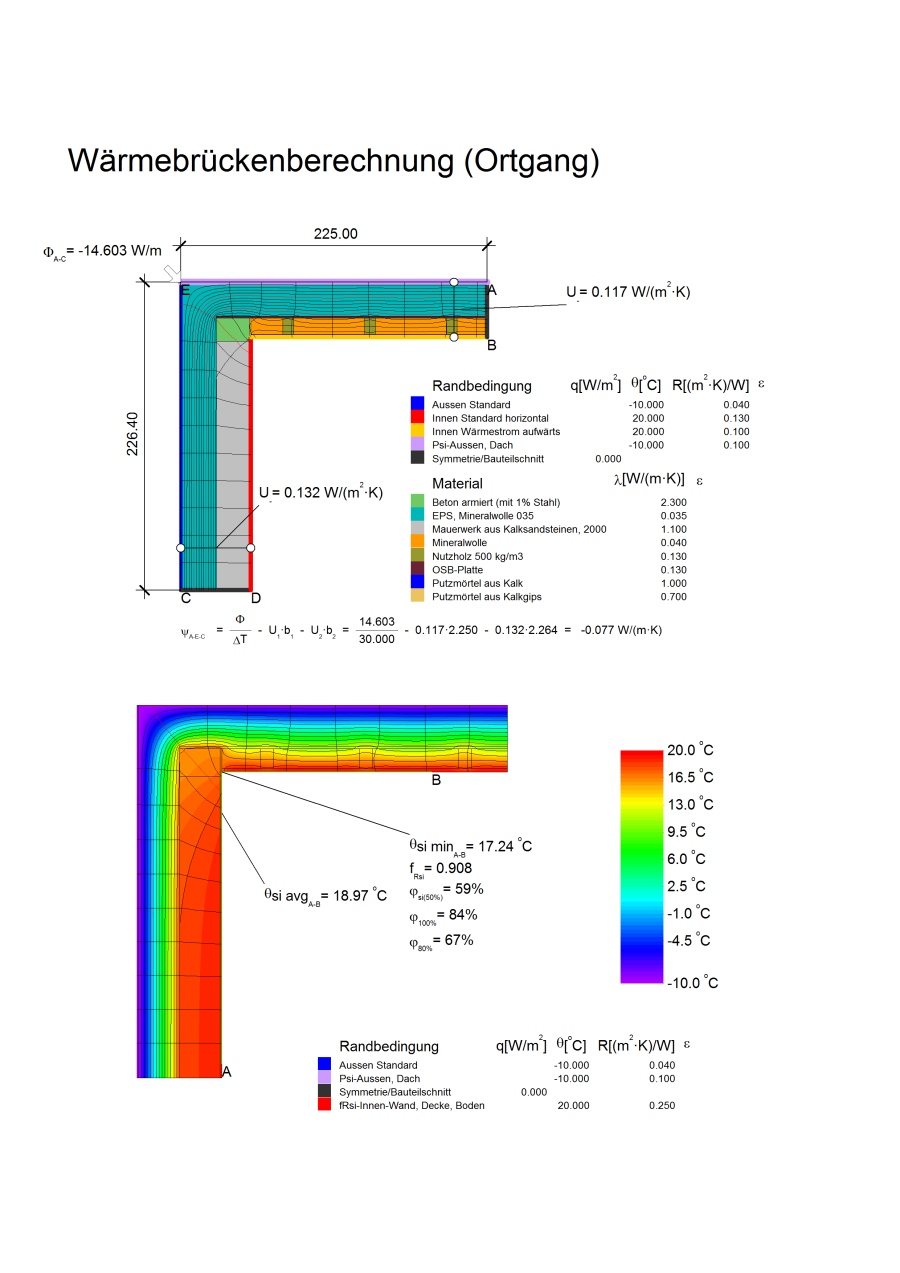
Nachfolgend ist die Wärmebrückenberechnung eines Ortgang Details dargestellt.
Zurück zu Definition und Auswirkungen von Wärmebrücken 🌡️
Zurück zur Übersicht Bauphysik Wärme 🌡️