Inhaltsverzeichnis
Unbeheizter Keller
Grundlagen
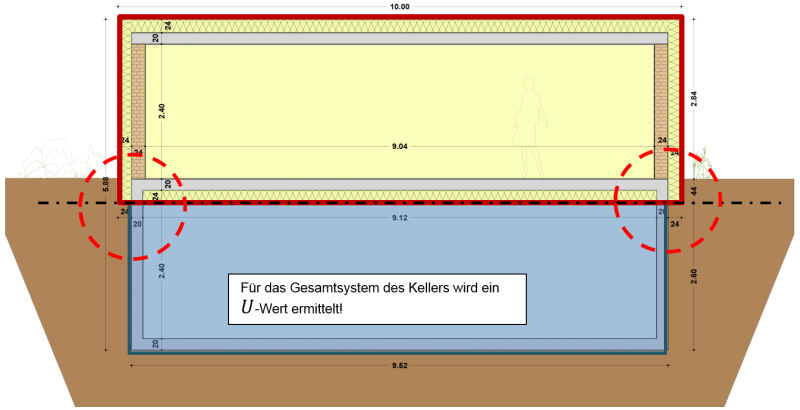
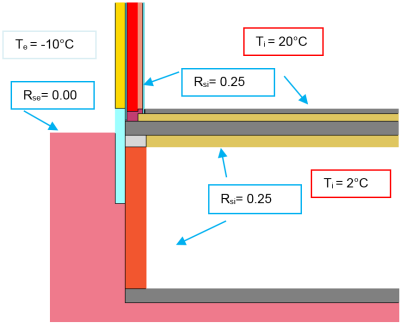
Unbeheizte Keller werden nicht aktiv temperiert. In ihnen herrschen in der Regel niedrigere Temperaturen. Es ist deshalb notwendig, den Keller thermisch vom beheizten Teil des Gebäudes zu trennen. In Energiebilanzierungen wird der unbeheizte Keller nicht in der Energiebezugsfläche berücksichtigt. Er stellt jedoch einen zusätzlichen Wärmeübergangswiderstand zwischen dem beheizten Innenraum und der Außenluft dar, der berücksichtigt werden muss.
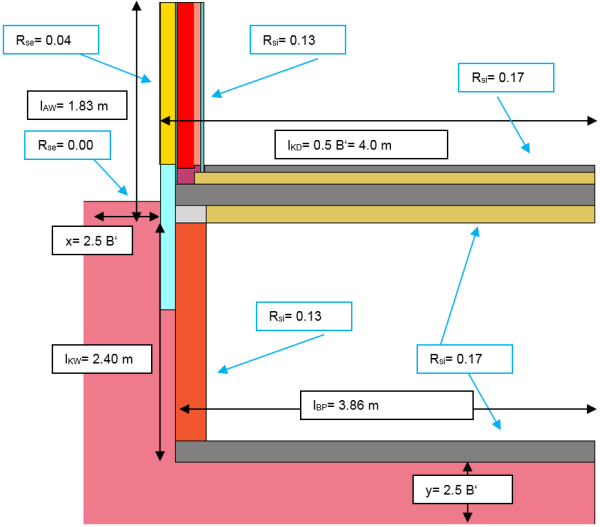
Dieser Übergangswiderstand wird der Grenzfläche zwischen dem Keller und dem Innenraum zugeordnet (siehe Abbildung oben). Ausgedrückt wird er durch folgenden U-Wert:
$$
\large{\dfrac{1}{U} = \dfrac{1}{U_f} + \dfrac{A}{(A \cdot U_{bf}) + (z \cdot P \cdot U_{bw}) + (h \cdot P \cdot U_W) + (0{,}33 \cdot n \cdot V)}}
$$
Gleichung 1 nach DIN EN ISO 13370, Kapitel 9.4
Dabei ist $U_f$ der Wärmedurchgangskoeffizient der Kellerdecke. $U_{bf}$ und $U_{bw}$ sind die U-Werte der Keller-Bodenplatte bzw. der Kellerwand und basieren wiederum auf den Näherungsfunktionen der Norm zur Berücksichtigung des Erdreiches. $U_W$ ist der U-Wert einer Kellerwand oberhalb des Erdreichs. Zusätzlich wird die Belüftung des Kellers berücksichtigt. Um die Anschluss-Situation zwischen Kellerraum und Innenraum energetisch bewerten zu können, muss für die Bilanzierung noch ein Ψ-Wert ermittelt werden. Dafür existieren mehrere Vorgehensweisen, die an folgendem Beispiel Detail gezeigt werden:
Normative Vorgehensweise
Leitwertbestimmung
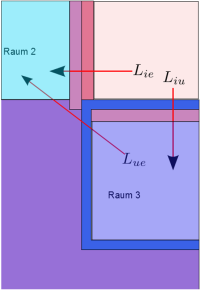 Analog zu Bodenplatte und beheiztem Keller muss auch für den unbeheizten Keller der Gesamtleitwert $L_{2d}$ berechnet werden. Der benötigte Wärmestrom aus dem beheizten Raum setzt sich aus den Leitwerten $L_{ie}$ und $L_{iu}$ zusammen:
Analog zu Bodenplatte und beheiztem Keller muss auch für den unbeheizten Keller der Gesamtleitwert $L_{2d}$ berechnet werden. Der benötigte Wärmestrom aus dem beheizten Raum setzt sich aus den Leitwerten $L_{ie}$ und $L_{iu}$ zusammen:
$$ \Large{\Phi = L_{iu} \cdot (\theta_i - \theta_u) + L_{ie} \cdot (\theta_i - \theta_e)} $$
Die Raumtemperatur $\theta_u$ des Kellers ist allerdings nicht bekannt, somit kann $L_{2d}$ nicht direkt berechnet werden. Es ist aber möglich, unter Verwendung von $L_{ue}$ den Wärmstrom bzw. den Leitwert durch folgende Gleichung auszudrücken:
$$ \Phi = \left(\frac{L_{iu} \cdot L_{ue}}{L_{iu} + L_{ue}}\right) + L_{ie}) \cdot (\theta_i - \theta_e) \quad \Rightarrow \quad L_{2d} = \left(\frac{L_{iu} \cdot L_{ue}}{L_{iu} + L_{ue}} + L_{ie}\right) $$
Es gilt also $L_{ie}$ , $L_{iu}$ und $L_{ue}$ zu ermitteln. Hierfür bestimmt man zunächst die Leitwerte der einzelnen Teil-Räume und löst folgendes Gleichungssystem:
$$ \begin{matrix} & \begin{matrix}L_{iu}&L_{ie}&L_{ue}\end{matrix} \\\\ \begin{matrix}L_1\\\\L_2\\\\L_3\end{matrix} & \begin{pmatrix}1\quad&1\quad&0\quad\\\\0\quad&1\quad&1\quad\\\\1\quad&0\quad&1\quad\end{pmatrix}\\\\ \end{matrix} \quad \Rightarrow \quad \begin{matrix} L_{iu} = 0{,}5 \cdot (L_1-L_2+L_3) \\ L_{ie} = 0{,}5 \cdot (L_1+L_2-L_3) \\ L_{ue} = 0{,}5 \cdot (-L_1+L_2+L_3) \end{matrix} $$
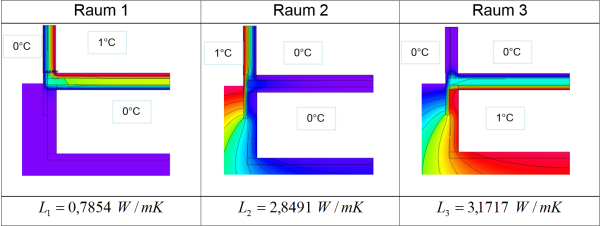
Um die Leitwerte der einzelnen Räume direkt aus dem Wärmestromprogramm ablesen zu können, ist es sinnvoll, die Temperaturen so zu wählen, dass die Temperaturdifferenz zu den jeweils benachbarten Räumen ein Kelvin beträgt. Die Ermittlungen werden am gegebenen Beispiel gezeigt:
Leitwertbestimmung $ \Large{_{2d}} $
$$\large{ L_{iu} = 0{,}5 \cdot (L_1-L_2+L_3) = 0{,}5540 \, \frac{\text{W}}{\text{m} \cdot \text{K}} \\ L_{ie} = 0{,}5 \cdot (L_1+L_2-L_3) = 0{,}2314 \, \frac{\text{W}}{\text{m} \cdot \text{K}} \\ L_{ue} = 0{,}5 \cdot (-L_1+L_2+L_3) = 2{,}6177 \, \frac{\text{W}}{\text{m} \cdot \text{K}}} $$
$$ \large{L_{2d} = \left(\frac{L_{iu} \cdot L_{ue}}{L_{iu} + L_{ue}} + L_{ie}\right) = 0{,}6886 \, \frac{\text{W}}{\text{m} \cdot \text{K}}} $$
Ψ-Wert-Ermittlung
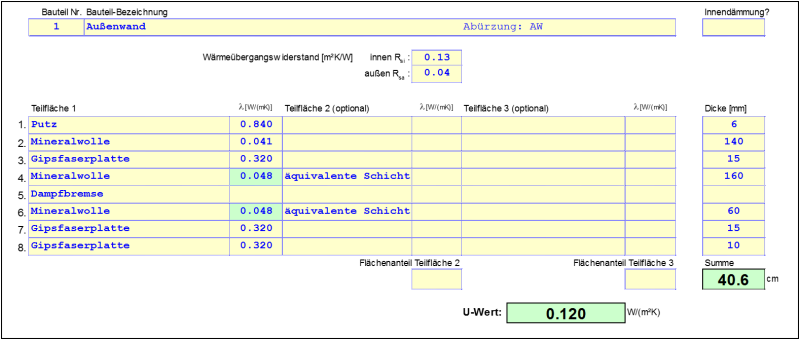
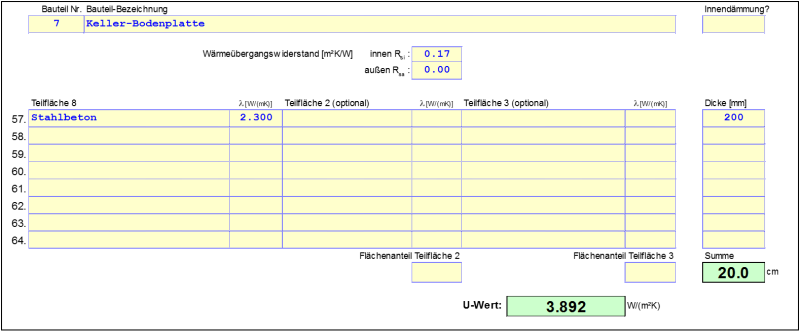
Nach Gleichung 1 wird der Ersatz U-Wert des Kellergeschosses berechnet:
$$\dfrac{1}{U} = \dfrac{1}{U_f} + \dfrac{A}{A \cdot U_{bf} + A_{bw} \cdot U_{bw} + A_W \cdot U_W + 0{,}33 \cdot n \cdot V} \quad \Rightarrow \quad U = 0{,}1273 \, \dfrac{\text{W}}{\text{m}^2 \cdot \text{K}}$$
Der Wert kann bei Eingabe der Eckdaten aus dem Erdreichblatt des PHPP entnommen werden, wobei einige Zeilen im Erdreichblatt erst eingeblendet werden müssen. Die Ψ-Wert Ermittlung erfolgt nun nach DIN EN ISO 10211 durch folgende Formel:
$$\Psi_g = L_{2d}-l_{AW} \cdot U_{AW}-0{,}5 \cdot B' \cdot U$$
Ψ-Wert Ermittlung
$$\Psi_g = 0{,}689 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}} \, - \, 1{,}830 \, \text{m} \, \cdot \, 0{,}120 \, \dfrac{\text{W}}{\text{m}^2 \cdot \text{K}} \, - \, 0{,}5 \, \cdot \, 8 \, \text{m} \, \cdot \, 0{,}1273 \, \dfrac{\text{W}}{\text{m}^2 \cdot \text{K}} = -0{,}042 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}}$$
Bei dieser Vorgehensweise wird angenommen, dass die außenmaßbezogene Grundfläche A des Kellergeschosses mit der Grenzfläche der Geschossdeckenfläche übereinstimmt, was natürlich meistens nicht zutreffend ist. Der Unterschied zur Realität wird also unter anderem durch den Ψ-Wert mit abgebildet.
Vorgehensweise nach Protokollband 27
Leitwertbestimmung
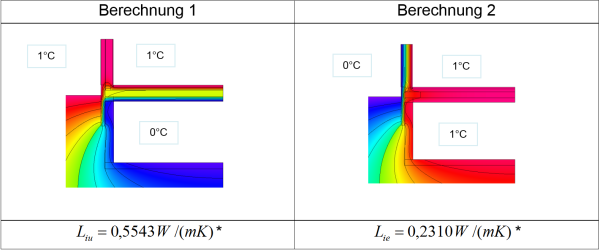
Eine alternative Vorgehensweise ist im Protokollband 27 des Arbeitskreises kostengünstige Passivhäuser enthalten und wird nachfolgend gezeigt. Für dieses Verfahren werden nur die Leitwerte $L_{ie}$ und $L_{iu}$ benötigt. Diese können mit zwei Berechnungen ermittelt werden. Die L-Werte entsprechen dabei jeweils dem Wärmestrom über die Begrenzungsflächen des beheizten Raums.
* Bei 1 K Temperaturdifferenz hat der Leitwert denselben Zahlenwert wie die Summe der Wärmeströme über alle Innenoberflächen des Innenraumes.
Anmerkung! Hier wurden $L_{ie}$ und $L_{iu}$ im Gegensatz zur vorherigen Variante mit nur 2 Simulationen ermittelt. In diesem Fall müssen die gesuchten Wärmeströme als Teil des gesamten Wärmestroms im Modell ermittelt werden, was je nach verwendeter Software relativ unübersichtlich oder gar nicht möglich ist. Alternativ können die Leitwerte wie in der vorherigen Variante bestimmt werden, dann aber wieder mit Hilfe von drei Simulationen.
Ψ-Wert Bestimmung
Der Leitwert $L_{iu}$ wird nun der Bodenplatte zugeordnet, $L_{ie}$ der Außenwand. Der Effekt der Wärmebrücke wird daher durch zwei Ψ-Werte ausgedrückt. Für die Außenwand gilt:
Ψ-Wert (Anteil Außenwand)
$$ \large{\Psi_g = L_{ie}-l_{AW} \cdot U_{AW}} $$
$$ \large{\Psi_{Außenwand} = 0{,}231-1{,}830 \cdot 0{,}120 = 0{,}0114} $$
Für die Bodenplatte:
Ψ-Wert (Anteil Bodenplatte)
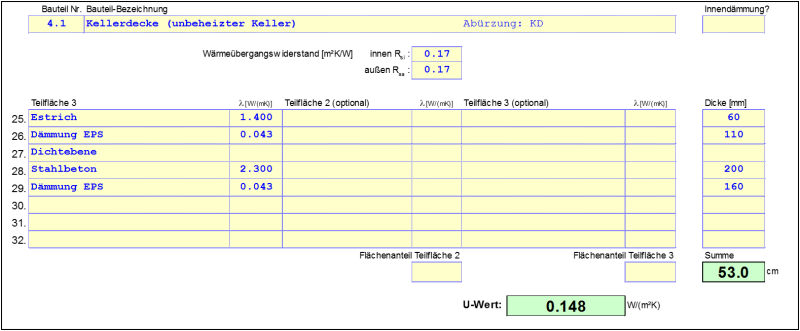
$$ \large{\Psi_g = L_{iu}-0{,}5 \cdot B' \cdot U_{Kellerdecke}} $$
$$ \large{\Psi_{Kellerdecke} = 0{,}5543-0{,}5 \cdot 8 \cdot 0{,}148 = -0{,}0377} $$
$\Psi_{Außenwand}$ wird im PHPP als normale Wärmebrücke eingetragen. Mit $\Psi_{Kellerdecke}$ wird im Erdreichblatt $U_f$ der Kellerdecke korrigiert, um anschließend mit Hilfe der Näherungsfunktionen den Gesamtwiderstand des Kellergeschosses auszurechnen.
$$ \large{U_{f,korrigiert} = U_f + \dfrac{\Psi_{Kellerdecke} \cdot P}{A}} $$
Bestimmung der minimalen Oberflächentemperatur und des f_Rsi-Faktors
Generell ist die Beurteilung der minimalen Oberflächentemperaturen und die Bestimmung des $f_{Rsi}$-Faktors anhand von stationären Berechnungen erdberührter Bauteile nur von begrenzter Aussagekraft, da Wärmespeicherung und Phasenverschiebung im Erdreich nicht berücksichtigt werden. Zusätzlich ist im Rahmen einer Bauteilzertifizierung die spätere Kellergröße nicht bekannt. Aus diesen Gründen sind Aussagen über Temperaturen, die sich in unbeheizten Kellerräumen einstellen, sehr schwierig. Das PHI empfiehlt für stationäre Berechnungen folgende Vorgehensweise:
Um die Temperatur des unbeheizten Kellers zu berechnen, wird ein Temperaturkorrekturfaktor von $f_x=0{,}5$ verwendet. Damit ergibt sich folgende Kellertemperatur:
$$ \large{\theta_{Keller} = \theta_i-f_x \cdot (\theta_i - \theta_e) = 20 \, ^\circ C - 0{,}5 \cdot (20 \, ^\circ C - (-10 \, ^\circ C)) = 5 \, ^\circ C} $$
Diese 5 °C werden nun als Temperaturrandbedingung im Keller verwendet. Auf Grund von Schränken und anderen Sperrgegenständen sollte auch hier der erhöhte Wärmeübergangswiderstand $R_{si} = 0{,}25 \, \frac{\text{m}^2\cdot \text{K}}{\text{W}}$ verwendet werden.
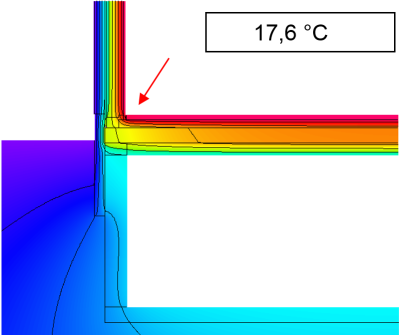
Bestimmung der minimalen Oberflächentemperatur und $ \Large{f_{Rsi}} $
$$ \large{f_{Rsi} = \dfrac{17{,}6 - (-10)}{20-(-10)}=0{,}92} $$
Ein einfacher Weg, um in konkreten Bauprojekten Oberflächentemperaturen mittels stationärer Berechnungen abzuschätzen, besteht darin, für die Temperatur des unbeheizten Kellers die Heizlast-Auslegungstemperatur aus dem Blatt Erdreich im PHPP zu verwenden. Vor allem bei ungedämmten Kellerdecken und großen Kellern ergeben sich damit deutlich höhere und realistischere Kellertemperaturen als mit pauschalen Reduktionsfaktoren.
Information! Normativ ist der $f_{Rsi}$–Faktor für Wärmebrücken mit drei Temperaturrandbedingungen nicht definiert. Die DIN EN ISO 10211 fordert dann die Angabe von Temperaturkorrekturfaktoren, mit denen es möglich ist, die minimale Oberflächentemperatur für jede beliebige Kombination der Raumtemperaturen zu bestimmen. Jedoch ist in diesem Fall die Kellertemperatur über $f_x$ an $\theta_i = 20 \, ^\circ C$ und $\theta_e = -10 \, ^\circ C$ gekoppelt, somit kann auch hier ein $f_{Rsi}$*-Faktor angegeben werden.