Inhaltsverzeichnis
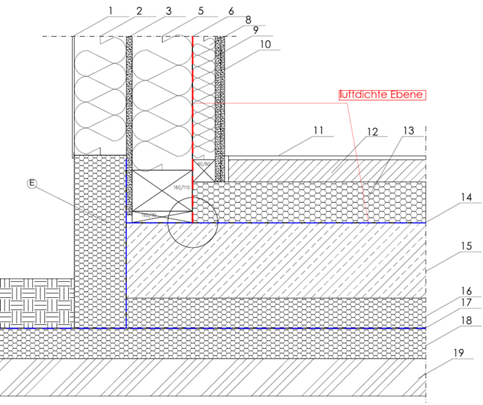
Außenwand auf Bodenplatte
Nachfolgend ist ein typisches Anschlussdetail dargestellt:
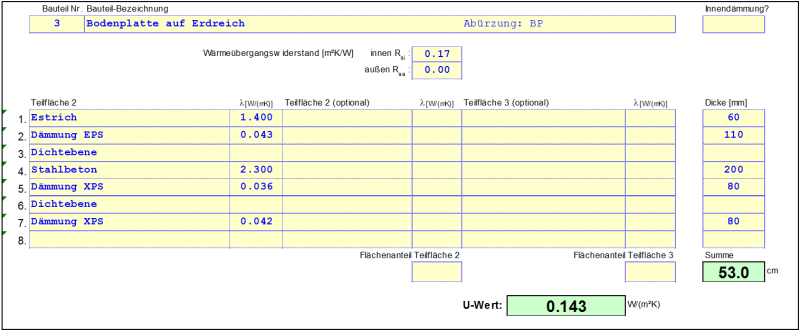
Anmerkung! Vor der Erstellung der Berechnungsmodelle ist zu prüfen welche Bauteilschichten für die Berechnungen relevant sind und welche vernachlässigt werden können. So können beispielsweise Sauberkeitsschichten, die aufgrund ihres Materials oder aufgrund ihrer Wasserdurchlässigkeit keine nennenswerte Dämmwirkung erzielen, vernachlässigt werden. Ebenfalls zu beachten ist, ob für Perimeter-Dämmungen, die außerhalb von Sperr- oder Dichtungsebenen liegen, schlechtere Bemessungswerte gelten.
Für das gegebene Beispiel wird der Unterbeton (Schicht Nr. 19) vernachlässigt, da die Dämmwirkung im Vergleich zum umliegenden Normerdreich gering ausfällt. Die Perimeter-Dämmung (Schicht Nr. 18) liegt außerhalb der Feuchtigkeitssperre (Schicht Nr. 17) und hat damit gemäß ihrer Zulassung einen schlechteren Bemessungswert der Wärmeleitfähigkeit. Für die Außenwand ergibt sich folgender U-Wert:
Berechnungsmodell
Zunächst wird das Gesamtmodell zur Berechnung des Leitwertes $L_{2d}$ erstellt. Falls die tatsächliche Gebäudegröße nicht bekannt ist, kann B‘ für die Option B beliebig gewählt werden, sollte aber nicht zu klein ausfallen. ($B' > 5 \, \text{m}$). Hier wurde $B' = 7{,}992 \, \text{m}$ gewählt (inklusive der Außenwand) [Anm.: Bei einigen Wärmestromprogrammen kann es vorkommen, dass es bei Maßen in den Modellen zu unbequemen Nachkommastellen kommt. Das ist jedoch nicht weiter von Bedeutung]. Die Bodenplatte wird nur bis zur Symmetrieachse modelliert und hat damit die Länge $\frac{B'}{2}=4{,}996 \, \text{m}$. Die Höhe der Außenwand sollte das Dreifache des zu untersuchenden Bereichs betragen. Wichtig ist, dass die Länge außenmaßbezogen, also bis an die Unterkante der Perimeter-Dämmung gemessen wird. In der zugehörigen PHPP-Berechnung ist derselbe Maßbezug zu verwenden. Im gezeigten Beispiel beträgt die Länge der Außenwand 2,03 m. Der Erdreichblock ist mindestens mit einer Abmessung von $2{,}5 \cdot B'$ zu modellieren. In der folgenden Darstellung sind alle relevanten Maßbezüge und Randbedingungen enthalten. Für die Bestimmung der Leitwerte ist es letztendlich egal, welche Temperatur-Randbedingungen angesetzt werden, es ist jedoch zu empfehlen, diejenigen anzusetzen, die später gebraucht werden, um die Oberflächentemperaturen zu bestimmen. Im unteren Teil ist die Ermittlung des Leitwertes $L_{2d}$ gezeigt, dieser resultiert aus dem mit dem Wärmestromprogramm berechneten Wärmestrom.
Leitwertbestimmung $ \Large{L_{2d}} $
$$ \large{\dot{q} = 19{,}488 \, \frac{\text{W}}{\text{m}}} \\ $$
$$ \large{L_{2d} = \frac{\dot{q}}{T_i-T_e} = \frac{19{,}488}{30} = 0{,}6496 \, \frac{\text{W}}{\text{m} \cdot \text{K}}} $$
Als nächstes muss der Leitwert der Bodenplatte bestimmt werden. Nach Option B in der Norm erfolgt dies, wie bereits erwähnt, durch eine zusätzliche Simulation. In DIN EN ISO 10211 wird dazu die Außenwand entfernt und durch eine adiabatische Grenze ersetzt. Besser ist es, die Bodenplatte in der Berechnung nur noch durch ihren Übergangswiderstand zu berücksichtigen. Dazu wird auf dem gegebenen Erdreichblock der Übergangswiderstand mit der entsprechenden Länge (hier im Beispiel mit $l_{BP}=3{,}996 \, \text{m}$) abgebildet. Da DIN EN ISO 13370 ebenso wie das PHPP von Bodenplatten ausgehen, die auf dem Erdreich liegen, liegt auch dieser Übergangswiderstand auf Höhe der Oberkante Erdreich, obwohl die Bodenplatte einige Zentimeter ins Erdreich hineinreicht. Damit wird erreicht, dass der resultierende Ψ-Wert mit den zugeordneten Grundannahmen zum Berechnungsansatz des PHPP passt.
Leitwert der Bodenplatte $ \Large{L_{BP}} $
$$ \large{\dot{q} = 14{,}023 \, \frac{\text{W}}{\text{m}}} \\ $$
$$ \large{L_{BP} = \frac{\dot{q}}{T_i-T_e} = \frac{14{,}023}{30} = 0{,}4674 \, \frac{\text{W}}{\text{m} \cdot \text{K}}} $$
Nun wird der Leitwert der Außenwand ermittelt. Anschließend kann, wie nachfolgend gezeigt, der Ψ-Wert des gesamten Anschlusses berechnet werden:
Leitwert der Außenwand $ \Large{L_{AW}} $
$$ \large{U_{AW} = 0{,}1205 \, \frac{\text{W}}{\text{m}^2 \cdot \text{K}}} $$
$$ \large{L_{AW} = l_{AW} \cdot U_{AW} = 2{,}03 \cdot 0{,}1205 = 0{,}2446 \, \frac{\text{W}}{\text{m} \cdot \text{K}}} $$
Ψ-Wert Ermittlung
$$ \large{\Psi = L_{2d}-L_{AW}-L_{BP}=0{,}6496-0{,}2446-0{,}4674=-0{,}062 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}}} $$
In der Praxis sollten zur Vereinfachung vorgefertigte Excel-Vorlagen zur Bestimmung der Ψ-Werte verwendet werden. Man kann dort die Wärmeströme und die notwendigen Längen eintragen und erhält direkt den gesuchten Ψ-Wert als Ergebnis.
Anmerkung zum Ergebnis! Der relativ stark negative Ψ-Wert kommt unter anderem dadurch zustande, dass die gegebene Dämmschürze im Ψ-Wert mit abgebildet wird. Dem Bearbeiter sollte bewusst sein, dass der hier gezeigte Ψ-Wert nicht nur den geometrischen Wärmebrückeneffekt im klassischen Sinn enthält, sondern auch neben der Dämmschürze noch weitere Effekte mit einschließt. So berücksichtigt der Ψ-Wert in diesem Beispiel auch, dass die Bodenplatte etwas im Erdreich versenkt ist und damit auch ein kleiner Teil der Außenwand im Erdreich liegt.
Achtung! Weist der zu berechnende Anschluss eine Dämmschürze auf, wird der Einfluss mit im Ψ-Wert abgebildet. Im PHPP darf daher die Randdämmung nicht zusätzlich eingetragen werden, da sie ansonsten doppelt berücksichtigt würde.
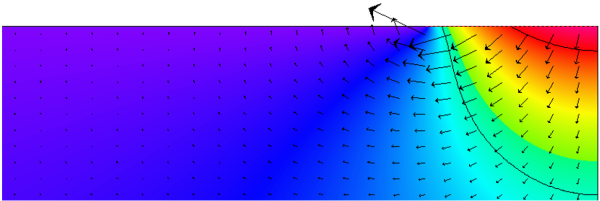
Bestimmung der Oberflächentemperatur
Zur der Bestimmung der minimalen Oberflächentemperatur und des $f_{Rsi}$-Faktors kann in diesem Fall wie bei jeder anderen Wärmebrücke vorgegangen werden.
Bestimmung der minimalen Oberflächentemperatur und $ \Large{f_{Rsi}} $
$$ \large{f_{Rsi \, = \, 0{,}25} = \frac{17{,}4-(-10)}{20-(-10)} = 0{,}91} $$