Einkapazitäten-Gebäudemodell
Ausgestattet mit den Kenntnissen zum Wärmetransport und den Gleichungen für das Verhalten eines beheizten Speichers (vgl. die vorausgehenden Abschnitte) können wir hier ein einfaches Modell für ein gesamtes Gebäude einführen, das überraschend gute Näherungen an das tatsächliche Gebäudeverhalten erlaubt und von dem aus viele Vorgänge im Zusammenhang mit passiv solaren Gewinnen und ihre Nutzbarkeit, Auswirkung einer zeitweisen Reduzierung der Heizung (z.B. Nachtabsenkung) und Möglichkeiten der Vermeidung von sommerlicher Überhitzung transparent und gut verständlich werden. Bessere Modelle sind in aller Regel zusammengesetzt aus vielen einzelnen solcher „Einkapazitätenmodelle“; wobei die Kunst dann gerade darin besteht, das Gesamte am Ende noch überschaubar zu halten. Die erreichbare Genauigkeit nimmt mit den verfeinerten Modellen natürlich zu - möglich ist aber immer nur die Verbesserung, zu der die betreffenden verfeinerten Daten auch zuverlässig verfügbar sind. Die grundlegenden Phänomene lassen sich bereits mit dem hier eingeführten sehr einfachen Modell verstehen.
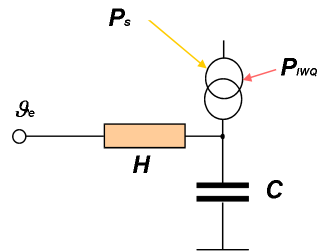
Die Abbildung rechts illustriert das Modell: Es ist tatsächlich nichts anderes als der bereits behandelte „beheizte Speicher“. Insbesondere nicht allzu schlecht wärmegedämmte Gebäude lassen sich mit gutem Erfolg auf ein derartiges Modell reduzieren: $C$ ist hier einfach die gesamte von den Innenoberflächen her thermisch zugängliche Gebäude-Kapazität1). Wie tief liegende Speichermassen zu jeweils welchem Anteil hier „mitgezählt“ werden, ist eine Wissenschaft für sich. Allerdings: Ein paar Dinge sind durchaus klar, alle oberflächennahen Bauteile wie Möbel, Estrich, Innenverkleidungen von Wänden, Innenwände, massive Teile der Außenwände - das zählt alles mit und wird einfach aufsummiert; jedenfalls so lange, wie sich zwischen den Einzelkapazitäten und dem Innenraum keine nennenswerten Dämmschichten befinden. Wie wir später noch sehen werden, muss es keine große Angst wg. eventueller Abweichungen bei der genauen Bestimmung von $C$ geben.
Das zweite, wesentliche Bestimmungsstück ist der gesamte Gebäudeleitwert $H$ zur Umgebung, die ist wiederum charakterisiert durch die Temperatur Umgebungstemperatur $\vartheta_e$.2)
Die solare Einstrahlung $P_s$ bestimmen wir wie im Kapitel über die Solarstrahlung beschrieben durch Aufsummierung aller direkten und indirekten solaren Strahlungsbeiträge. Dazu kommt die Summe der innen wirksamen inneren Wärmequellen $P_{IWQ}$. Die Heizleistung $P_H$ wird über geeignete Regelalgorithmen angesetzt. Alle drei Gewinn-Wärmeströme werden aufsummiert und direkt in die Kapazität eingespeist. An solchen Stellen kann das Modell leicht sorgfältig verfeinert werden, in dem z.B. gesonderte Wärmeübergänge, auch zeit- und/oder temperaturabhängige, verwendet werden3). Wir halten es hier zunächst bewusst so einfach wie möglich. Zeitabschnittsweise halten wir dabei auch alle Randbedingungen fest: D.h., es gibt für jeden Zeitabschnitt jeweils eine konstante Außentemperatur, Solarstrahlung, Heizleistung etc.. Weil die Zeitabschnitte im Grundsatz beliebig klein gewählt werden können4), bedeutet Letzteres kaum eine Einschränkung für das Modell. Das wirklich Schöne an diesem Modell ist, dass die Modellgleichung, nämlich [iSpDGL], vgl. die Herleitung in "der beheizte Speicher", für jeden Zeitabschnitt die dort schon angegeben exakte analytische Lösung hat. Diese können dann wieder stückweise aneinandergesetzt werden.
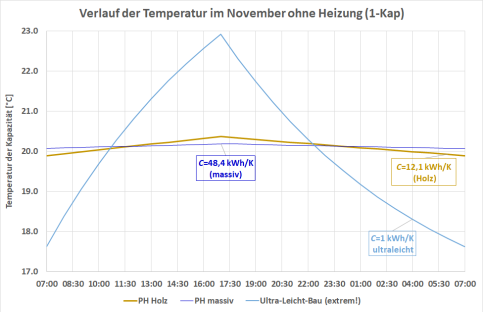
Um zu illustrieren, wie sich Gebäude thermisch verhalten, zeigen wir Temperaturverläufe an einem typischen Tag im November5) mit 8°C Außentemperatur und insgesamt 4,08 kWh solarem Wärmeeintrag zwischen 7:00 und 17:00. Um deutlich herausstechen zu sehen, welchen Einfluss die Dynamik auf das Ergebnis hat, haben wir dabei ein Objekt mit nur extrem geringer raumseitiger Wärmekapazität, nämlich insgesamt 1 kWh/K, berechnet. Das entspräche dem Fall, dass alle innenseitigen Oberflächen inkl. der Böden nur über eine 5 mm dünne Innenverkleidung verfügen; das ist natürlich kein realistisch gebautes Gebäude, solche haben mindestens 3 bis 4 mal soviel thermische Kapazität6). Mit einer so extrem geringen inneren Wärmekapazität beträgt die Zeitkonstante dieses Gebäudes nur 12 h; dadurch lässt sich der exponentielle Temperaturabfall ab 17:00 von 22,9°C auf 18,4°C gut erkennen7). Trotzdem werden selbst damit die Grenztemperaturen (27°C am Tag und 15,2°C in der Nacht) nicht entfernt erreicht: Auch dieses Gebäude ist noch träge genug, auch im November die Temperaturen im Innern in einem akzeptablen Bereich zur halten, auch wenn keine Heizung betrieben wird. Ein realistisch gebautes Holzhaus mit innerliegenden aussteifenden Platten8) an den Außenbauteilen, Dielenböden mit Split- oder Magerbeton-Füllung und üblicher Möblierung kommt bereits auf rund 12,1 kWh/K innere Wärmekapazität, wodurch die Zeitkonstante hier auf 146 h ansteigt. Unter diesen Umständen sind die Tag/Nacht-Einflüsse im Diagramm (braune Linie) zwar noch erkennbar, sie sind aber ziemlich unbedeutend: Das Maximum liegt bei 20,37°C, das Minimum bei 19,95°C. Die Temperaturen bleiben so weit von den Gleichgewichts-Grenztemperaturen9), dass die Steigung der Temperatur kaum wahrnehmbar ist und der exponentielle Verlauf nicht deutlich erkennbar ist, da er in diesem Intervall fast linear verläuft. Im dritten dargestellten Fall, ein Passivhaus in Massivbauweise mit 48,4 kWh/K innerer Wärmekapazität und weiterhin gleichem Wärmeschutz beträgt die Zeitkonstante nun 583 h und die Temperaturen bewegen sich kaum merklich zwischen 20,07 und 20,19°C.
Bereits aus dem ersten hier behandelten Fall wird deutlich: Die in normalen Gebäuden in Mitteleuropa vorhandene Wärmekapazität reicht, auch bei reiner Holzbauweise, im hiesigen Klima aus, um die Tag-Nacht-Unterschiede im Außenklima für 24-Stunden-periodische Vorgänge so weit heraus zu glätten, dass der Komfort davon nicht beeinträchtigt wird. Das gilt zumindest so lange, wie die Objekte über einen vernünftigen Wärmeschutz verfügen.
Das illustriert, weshalb wir gut zutreffende Ergebnisse bei Berechnungen auch bereits mit einem nur statischen Modell (ohne Wärmekapazitäten) bekommen, wenn mit den zeitlichen Mittelwerten der Randbedingungen über mehrere Tage (>3) gerechnet wird. Und es lässt zugleich erkennen, dass das Rechnen einer statischen Bilanz mit Momentanwerten der Temperaturen dagegen zu völlig irreführenden Ergebnissen führen kann.
Im folgenden Kapitel wollen wir das 1-Kapazitätenmodell auf einige interessante Fälle des Gebäudebetriebs anwenden:
weiter zu "einige Anwendungen des 1-Kapazitätenmodells" 🌡️
Zurück zu "der beheizte Speicher" 🌡️