U-Wert Mehrschichtaufbau

Mit den schon dargestellten Grundlagen kann nun auch leicht gezeigt werden, wie sich der U-Wert eines Wandaufbaus, der sich aus mehreren planparallelen Schichten zusammensetzt, aus den Dicken und den Wärmeleitfähigkeiten bestimmen lässt. 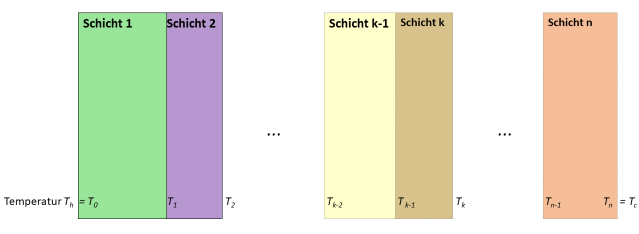Zunächst warten wir bei konstanter (auf der linken Seite) höheren Temperatur $T_h$ und der kalten Temperatur $T_c$ ganz rechts lang genug, bis sich überall ein Gleichgewicht eingestellt hat¹⁾. Wegen des ersten Hauptsatzes muss der Wärmestrom durch jede der Schichten dann überall gleich groß sein. Wäre er das nicht, dann würde die eine oder andere Schicht Wärme aufnehmen - und dann ist das Gleichgewicht noch nicht erreicht, denn bei dieser Schicht ändern sich dann die Messwerte. Die konstante Wärmestromdichte bezeichnen wir wieder mit $\dot{q}$. Die Temperaturen an den Schichtgrenzen bezeichen wir auf der kalten (rechten) Seite der Schicht $k$ mit $T_k$. Es sei weiter $T_0:=T_h$ und es ist natürlich für die letzte Schicht $T_n=T_c$ ganz am rechten Ende. Alle Temperaturen sind im Fließgleichgewicht konstant. Für die k-te Schicht sieht es daher so aus, als würde sie an zwei Temperaturreservoire mit Temperaturen $T_{k-1}$ (heiße Seite) und $T_k$ (kühle Seite) grenzen. Die durch sie fließende Wärmestromdichte können wir daher nach [U2] bestimmen:

$\dot{q} = U_k \cdot (T_{k-1}-T_k) \hspace{6cm} [U4]$

Wo jetzt $U_k$ der Wärmedurchlasskoeffizient der k-ten Schicht ist. Teilen wir das durch den Wert von $U_k$ (der ist nicht Null), so erhalten wir

${\displaystyle T_{k-1}-T_k = \frac{\dot{q}}{U_k} = {R_k} \cdot \dot{q} \hspace{5cm} [U5]}$ ,

wobei wir für den letzten Schritt den Wärmedurchlasswiderstand $R_k=\frac{1}{U_k}$ eingeführt haben. Wenn wir jetzt alle Temperaturdifferenzen der Schichten 1 bis n aufsummieren, heben sich alle Zwischentemperaturen aus dieser Summe heraus und es bleiben nur die Temperaturen der ursprünglichen Reservoire stehen

${\displaystyle T_{h}-T_c = R_1 \cdot \dot{q}+ R_2 \cdot \dot{q}+ ... + R_n \cdot \dot{q} \hspace{3cm} [U6]}$ ,

und aus dieser Summe können wir jetzt den gemeinsamen Faktor $\dot{q}$ ausklammern. So erhalten wir, dass der gesamte Wärmedurchlasswiderstand eines mehrschichtigen Bauteils gleich der Summe der einzelnen Wärmedurchgangswiderstände aller Schichten ist:

${\displaystyle R = R_1 + R_2 + ... + R_n \hspace{5,8cm} [U7]}$ ,

Wärmedurchlasswiderstände summieren sich also einfach auf. Wir können daraus auch durch Kehrwertbildung den resultierenden U-Wert $U$ des Gesamtaufbaus bestimmen:

${\displaystyle U = \frac {1} {R_1 + R_2 + ... + R_n} \hspace{5,8cm} [U8]}$ ,

Die einzelnen Schicht-R-Werte lassen sich nach [$\lambda 1$] aus den Einzelschichtdicken $d_k$ und den Materialeigenschaften (insb. Wärmeleitfähigkeiten) berechnen. Das ist auch die in der Normung dargestellte Berechnung des U-Wertes mehrschichtiger Bauteile.

${\displaystyle \hspace{2cm} R_k= \frac{d_k}{\lambda_k} \hspace{6.5cm} [\lambda 1]}$

Das lässt sich z.B. alles in ein Tabellen-Kalkulationsblatt packen - und dann ist der Berechnungsgang fixiert und neue „Varianten“ eines Aufbaus lassen sich schnell ermitteln. Im PHPP gibt es z.B. so ein Blatt „U-Werte“, das über noch ein paar weitere Möglichkeiten verfügt. Aber auch eine Rechnung „von Hand“ ist schnell ausgeführt, sobald die Dicken ausgemessen und die Stoffkennwerte nachgeschlagen sind.

Konsequenz: Jeder auch noch so schlechte U-Wert eines alten Bauteils lässt sich in der Praxis durch Zubau einer Dämmschicht nachbessern. Bei schlechten alten Werten bringen auch schon wenige cm oft eine ganze Menge (siehe z.B. unsere Anleitung zur Dämmung einer Heizkörpernische). Da in den meisten Fällen auf der Außenseite der Bauteile bei bestehenden Gebäuden durchaus eine Menge Platz ist und Dämmstoffe zu den billigsten und am leichtesten verarbeitbaren Baustoffen überhaupt gehören, lohnt es sich aber, ausreichend dicke Dämmschichten²⁾ auf das alte Bauteile aufzubringen. Damit reduzieren sich die Wärmeverluste, richtig ausgeführt, um Faktoren³⁾. Die entscheidenden Kosten solcher Maßnahmen sind genau genommen nur die „Rüstkosten“ - es muss meist ein Gerüst gestellt werden und natürlich eine Wetterschutzschicht auf der Außenseite. Da das aber alles ohnehin irgendwann einmal passiert, sei es nur, um die Fassade neu zu streichen, geht es dabei vor allem darum, diese Chancen jeweils auch zu nutzen um sich von kalten ungemütlichen Innenwandoberflächen und hohen Heizkosten zu befreien.

Hier gibt es eine Übung zu mehrschichtigen Aufbauten zum nachrechnen.

Weiter zum Kapitel Wärmeübergänge I 🌡️

Zurück zum Kapitel Wärmeleitfähigkeit 🌡️

Zurück zum Kapitel Einführung des U-Wertes 🌡️

Zurück zum Grundkurs Bauphysik Wärme - Übersicht 🌡️