Inhaltsverzeichnis
Wärmeübergänge II
Zusammensetzung Konvektion und Wärmestrahlung, insbesondere: Temperaturabhängigkeit
Nachdem wir den Mechanismus des Strahlungswärmeübergangs erklären und so dessen Werte für den Wärmeübergang sehr genau quantifizieren konnten, soll auch der Beitrag des konvektiven Wärmeübergangs noch einmal genauer betrachtet werden: Das erweist sich als weit komplexer und schon von daher nur mit geringerer Genauigkeit möglich1). Die folgenden Ausführungen beziehen sich damit zunächst einmal nur auf empirisch gewonnene Zusammenhänge; mit heutigen Mittel der CFD (Computational Fluid Dynamics) sind für klar beschriebene Einzelfälle nun durchaus noch genauere Berechnungen möglich - deren generelle Übertragung in die Praxis scheitert aber immer noch an der hohen Komplexität schon bei den Randbedingungen. Andererseits reichen die im Folgenden beschriebenen empirischen Näherungen für den weit überwiegenden Teil von Fragestellungen in der Bauphysik aus, insbesondere bei Gebäuden, die eine einigermaßen vernünftige Wärmedämmung aufweisen. Sehr viel größeren Einfluss haben die hier noch vorliegenden Unsicherheiten auf Wärmedurchgänge bei Zeltplanen oder Einfachscheiben.
Erzwungene Strömung: Z.B. äußerer 'e' konvektiver 'c' Wärmeübergang $h_{e,c}$
Der erzwungene Antrieb kann z.B. Wind sein, aber auch ein Gebläse, das Luft entlang eines Konvektors2) strömen lässt. Dabei geht es sowohl um den Geschwindigkeitsbetrag $v$ als auch dessen Richtung $\overrightarrow{v}/v$. Allerdings sind nur die extremen Werte dokumentiert verfügbar - die geben wir hier an.
| Formel für $h_{e,c}$ in W/(m²K) | WIND-Situation |
|---|---|
| ${\displaystyle 4 + 4 \frac{v}{\text{m/s}} }$ | parallele Anströmung |
| ${\displaystyle 6 + 6 \left( \frac{v} {\text{m/s}} \right)^{0,7} }$ | Luv (windzugewandt) |
| ${\displaystyle 6 + 1,4 \left( \frac{v} {\text{m/s}} \right) }$ | Lee (windabgewandt, < 8 m/s) |
Ein Beispiel: Bei schwachem Wind, 4 m/s, parallel angeströmt, der konvektive Wärmeübergang wird
$h_c = (4+4 \cdot 4) \text{W/(m²K)} = 20 \text{W/(m²K)} $.
Freie Konvektion (Wärmeübergang an inneren Oberflächen) $h_{i,c}$
Die freie Strömung wird angeregt durch die Temperaturdifferenz $\Delta \vartheta$ (anzugeben hier in K). Bei zunehmender Temperaturdifferenz nimmt der Dichteunterschied zu, so dass dann auch der Wärmetransport noch mehr zunimmt.
| Formel für $h_{i,c}$ in W/(m²K) | Lage bzgl. des Wärmestroms |
|---|---|
| ${\displaystyle 1,31 \Delta \vartheta^{0,33} }$ | vertikale Oberfläche |
| ${\displaystyle 1,89 \Delta \vartheta^{0,33} }$ | Wärmestrom nach oben |
| ${\displaystyle 0,4 \Delta \vartheta^{0,25} }$ | Wärmestrom nach unten |
Der Mechanismus: Auch wenn es keinen äußeren mechanischen Antrieb gibt, entsteht an einer Oberfläche mit gegenüber der Luft veränderter Temperatur3) eine Luftströmung: Durch den Wärmetransport durch Wärmeleitung wird die angrenzende Luft abgekühlt. Dadurch steigt ihre Dichte und dabei wird die Gewichtskraft größer als die Auftriebskraft: Die Luftschicht sinkt entlang der Oberfläche ab, es entsteht „freie Konvektion“4) . Die genauen Strömungsgeschwindigkeiten und -verteilungen hängen auch von den Ausdehnungen und Temperaturen anderer Bauteile ab; daher sind die oben angegeben empirischen Formeln eine Näherung - sie betrachten raumtypische Abmessungen (ca. 2.5 m hoch) ohne zusätzliche Möbel.
Die Genauigkeit der möglichen Angaben für konvektive Wärmeübergänge sind daher aus den verschiedensten Gründen begrenzt, vor allem, weil die genauen Randbedingungen oft im Einzelfall gar nicht bekannt sind. Für einfache Bilanzrechnungen, wie sie z.B. beim PHPP durchgeführt werden oder bei Einzelbauteilen bleiben wir in der Bauphysik daher in der Regel bei der näherungsweisen Angabe eines Summenwertes für konvektive und radiative Wärmeübertragung. Für die thermische Gebäudesimulation freilich wäre damit die Ungenauigkeit zu hoch: Da muss zwischen der Konvektion und der Strahlung klar getrennt werden, da dabei ja auch die Temperaturen der im Wärmeaustausch stehenden Systeme ganz unterschiedlich sein können. Wir behandeln im Folgenden einige Beispiele.
Beispiel 1: Wenn die Oberflächentemperatur einer Fläche bei 0°C5) in einem Raum mit 20°C Raumlufttemperatur liegt, dann ergibt sich für eine vertikale Fläche ein $h_{i,c}$ = 3,52 W/(m²K); bei einer Temperaturdifferenz von nur 3 K geht der Wert auf etwa 1,87 W/(m²K) zurück6) .
Beispiel 1a (erweitert): Wir beziehen jetzt den Wärmeübergang durch Wärmestrahlung für die Fläche mit 0°C in einem Raum mit 20°C inneren Oberflächentemperaturen7) mit ein: Die Emissionsgrade werden mit 0,85 (für die Glasoberfläche) und 0,92 für die „Tapeten“ angesetzt (das ergibt einen Strahlungssichtfaktor von etwa $\phi = 0,79$. Mit dem Stefan-Boltzmannschen Gesetz ergibt sich der „Strahlungswärmeübergang“ daraus zu $h_{i,r}$ = 4,08 W/(m²K); auch bei einer sehr kalten Oberfläche einer Einscheibenverglasung ist dieser Wert immer noch bedeutender als der freie konvektive Übergang. Dabei mit zu bedenken ist: Der Strahlungsaustausch findet mit den anderen Oberflächen im Raum statt, der konvektive Wärmeübergang mit der Raumluft; eine 'Addition' der beiden Werte8) liefert um 7,6 W/(m²K) oder einen Wärmeübergangswiderstand auf der Innenseite von 0,13 m²K/W. Das ist gerade der auch in der Normung eingeführte „naive“ Wert, wenn stark vereinfacht gerechnet wird.
Bei einer Temperaturdifferenz von nur 3 K steigt der Strahlungswärmeübergang auf etwa 4,5 W/(m²K) an und die „naive Summe“ beider Wärmeübergang beträgt noch etwa 6,3 W/(m²K). Für gute gedämmte und daher warme Innenoberflächen ist die Dominanz der Wärmestrahlung noch ausgeprägter; die nur noch geringere Strahlungstemperaturdifferenz zu einer Dreischeiben-Wärmeschutzverglasung wird dann auch nicht mehr subjektiv als „kalt“ empfunden.
Freie Konvektion (Wärmeübergang zwischen zwei parallelen ebenen Oberflächen) ${\Lambda_{cc}}$
Der hier behandelte Fall kommt gerade bei Bauteilen ziemlich häufig vor: Zwei ebene Flächen stehen einander parallel gegenüber: D.h., sie haben überall den gleichen Abstand d. Wir haben einen ebenen Spalt orthogonal zum Wärmestrom. Um die Situation nicht zusätzlich zu verkomplizieren, gehen wir davon aus, dass der Spalt dicht ist, d.h. es gibt keinen Austausch des im Spalt vorhandenen Fluids mit der Umgebung - weder nach innen noch nach außen. Und wir wollen zunächst annehmen, dass der Spalt in den Richtungen senkrecht zum Wärmstrom nicht begrenzt ist - das ist in der Praxis natürlich nicht so, es stellt sich aber heraus, dass die daraus resultierenden Randeffekte später separat in guter Näherungen behandelt werden können und dass die Bedingung „unbegrenzt“ für die auschlaggebenden Eigenschaften des Wärmetransports schon bei etwa 10 bis 20-facher Ausdehnung der Querschnittsfläche gegenüber dem Spaltabstand d erfüllt ist. Wir behandeln hier zunächst einen lotrecht stehenden Spalt, d.h. die Richtung des Wärmstroms ist horizontal.
Beispiele:
Ein gutes Beispiel ist eine moderne 'versiegelte' Verglasungseinheit. Sie besteht aus mehreren ebenen Glasscheiben, die an den Rändern durch gasdicht versiegelte Abstandshalter auf dem konstanten Abstand d gehalten werden. In aller Regel ist der Zwischenraum mit einem Gas gefüllt, da Gase die niedrigsten in der Natur verfügbaren Wärmeleitfähigkeiten haben9).
Ein weiteres Beispiel ist ein Spalt in einem Wandaufbau, z.B. bei einem zweischaligen Mauerwerk, wenn dieser nur wenig 'belüftet' ist.
Wir überlegen zunächst qualitativ, welche Vorgänge hier stattfinden. Dazu beheizen wir die linke Oberfläche zum Spalt hin auf eine konstante Temperatur Th und kühlen die rechte Oberfläche auf Tc. Durch Wärmeleitung im Füllgas wird Energie von der linken Oberfläche in das Gas transportiert; je näher die Gasschicht an der Oberfläche ist, eine desto höhere Temperatur nimmt sie an; der Transport von Schicht zu Schicht erfolgt durch Wärmeleitung und solange keine makroskopische Bewegung (Strömung) im Gas zustande kommt, gibt es auch nur diese Wärmeleitung. Den Wärmetransport durch Wärmeleitung in einer Schicht der Gesamtdicke d können wir, wie schon zuvor beschrieben, durch einen Wärmedurchlasskoeffizienten
${\displaystyle \Lambda_{cond} = \frac{\lambda}{d}} $
bestimmen.
Zugleich nimmt aber auch die Dichte der jetzt in der Nähe der beheizten Oberfläche erwärmten Luft ab: Diese erfährt eine Auftriebskraft; das Analoge, nur mit einer Dichtezunahme, erfolgt auf der kalten Seite. Die Auftriebskraft hält eine Luftströmung, zunächst sauber vertikal, entgegen der Reibungskräfte in der Luft in Gang; solange der Antrieb gering genug ist, handelt es sich um eine rein laminare Strömung, d.h. um parallel gegeneinander verschobene Luftschichten - es gibt dann keine Horizontalkomponente der Geschwindigkeit, jedenfalls nicht im ungestörten Bereich des Spaltes; erst an der oberen und unteren Begrenzung wechselt dieser Luftstrom von der heißen auf die kalte Seite. Solange dies in dieser geordnet-laminaren Form geschieht, ist der zusätzliche Wärmeverlust dadurch vernachlässigbar. Das bedeutet, dass die Wärmeübertragung tatsächlich durch das oben berechnete $\Lambda_{cond}$ gegeben ist. Wird die Temperaturdifferenz größer (oder der Spaltzwischenraum größer), dann nimmt das Verhältnis von Trägheitskraft zu Reibungskraft zu; weiter von den Wandungen entfernte Luftpakete können jetzt unter geringerer Reibung auch horizontale Geschwindigkeitsanteile annehmen: Die Strömung wird im Inneren des Spaltes turbulent.
Die Erfahrungen mit den Verglasungen hat gezeigt, dass eine Auslegung der Scheibenabstände (= Dicke des gasgefüllten Spaltes) in der Weise, dass dort im Auslegungsfall rund 7,5 K Temperaturdifferenz auftreten, empfehlenswert ist. In Mitteleuropa bedeutet das mindestens 2 Gaszwischenräume10). Je nach Füllgas tritt dann turbulente Konvektion bei einem Grenz-Abstand $d_{Grenz}$ von rund
$d_{Grenz,Luft} =$ 19 mm Scheibenabstand(Luft),
$d_{Grenz,Ar}\; \; =$ 17,5 mm (Argon) und
$d_{Grenz,Kr}\; \; =$ 11 mm (Krypton)
auf. Bei kleineren Dicken und/oder kleineren Temperaturdifferenzen bleibt die Strömung laminar, d.h., es kann weiter $\Lambda_{cond}$ für den Wärmedurchlass im Gas angesetzt werden. Für größere Abstände d erweist sich das folgende Modell als überraschend gut geeignet: Es verblieben an beiden Oberflächen laminare Unterschichten, in denen sich das Gas nach wie vor nur mit vertikalen Geschwindigkeitskomponenten bewegt; dazwischen aber ist die Reibung so gering, dass turbulente Strömung vorliegt und der Wärmeübertrag um ein Vielfaches erhöht wird - im Vergleich zur sehr geringen Wärmeleitung im Gas können wir das wie einen thermischen Kurzschluss ansetzen. In immer noch guter Näherung kann die Gesamtdicke der laminaren Unterschichten in der Summe beider Seiten als zunächst konstant, und zwar gleich der Grenzdicke der noch vollständig laminaren Strömung angesehen werden.
Verwenden wir ein solches vereinfachtes Modell, so sinkt mit zunehmender Dicke des Spaltes der Wärmedurchlasskoeffizient zunächst umgekehrt proportional zur Dicke wie bei reiner Wärmeleitung und bleibt dann, mit noch weiter vergrößerten Abständen, annähernd konstant. Diese Werte werden durch
${\displaystyle \Lambda_{cc} = \frac{\lambda}{\text{Min}(d, d_{Grenz})}} $
hinreichend genau getroffen. Genauer lassen sich die Durchlasskoeffizienten mit Hilfe von Formeln aus der Ähnlichkeitstheorie der Fluiddynamik ermitteln - so ist das z.B. in [EN 673] beschrieben. Das untenstehende Diagramm vergleicht die Ergebnisse nach [EN 673] (durchgezogene Linien mit Symbolen) mit den durch die obige Gleichung gegebenen Näherungen (breite hellfarbene Kurven). Aufgetragen ist der kombinierte wärmeleitend/konvektive Wärmedurchgang $\Lambda_{cc}$ in W/(m²K) durch das Gas im Spalt über der Spaltdicke. Dabei beträgt die Temperaturdifferenz in jedem der Spalte etwa 7,5 K. Mit angegeben sind die Fehlergrenzen der Formeln nach der Ähnlichkeitstheorie; diese nehmen im turbulenten Bereich stark zu, allerdings sind solche großen Scheibenabstände von mehr als 20 mm ohnehin unüblich. Aus diesem Diagramm können empfehlenswerte Scheibenabstände für die Dreischeibenverglasung abgelesen werden, und zwar betragen diese rund 20 mm in Luft, 18 mm in Argon, und 12 mm in Krypton. Die zugehörigen optimalen Werte für $\Lambda_{cc}$ ergeben sich dann zu
| Füllgas | Luft | Argon | Krypton |
| empfohlene Dicke d / mm | 20 | 18 | 12 |
| Wärmedurchlassk. $\Lambda_{cc}$ W/(m²K) bei dieser Dicke und 7,5 K Temp.-Diff. | 1,28 | 0,94 | 0,75 |
| Wärmeleitf. des Füllgases W/(mK) | 0,250 | 0,168 | 0,09 |
Das Diagramm zeigt erwartungsgemäß, dass für alle drei Füllgase der Wärmedurchgang zunächst umgekehrt proportional zur Spaltdicke d abnimmt - es liegt tatsächlich weitgehend reine Wärmeleitung vor und alle Verfahren liefern in diesem Bereich auch gleiche Ergebnisse. Die Wärmeleitfähigkeiten von trockener Luft, Argon und Krypton unterscheiden sich dabei grob im Verhältnis 3:2:1. Alle drei Kurven gehen mit zunehmendem Scheibenabstand in das turbulente Strömungsregime über: Das ist bei den jeweiligen Grenzdicken der Fall. Ab diesen Punkten werden die Abweichungen zwischen den Verfahren größer. Da die Konvektion in Luft aber auch in Argon erst später einsetzt als in Krypton11), verhalten sich die Bestwerte der konvektiven Wärmedurchgangskoeffizienten wie 1,8:1,3:1,012). Dabei sind die Spaltdicken jeweils 20 mm (Luft), 18 mm (Ar) und 12 mm (Kr); es 'lohnt' sich also bei Luft und Argon, auf große Spaltbreiten zu gehen, während für Krypton maximal 12 mm sinnvoll sind. Während die Kosten für eine Füllung mit trockener Luft aber auch mit Argon vernachlässigbar gering sind, ist Krypton ein vergleichsweise knappes und viel gefragtes Edelgas - Kryptongefüllte Verglasungen sind deshalb spürbar teurer als solche mit Argon. Außer in speziellen Fällen wird sich die Verwendung von Krypton in Isoliergläsern kaum lohnen.
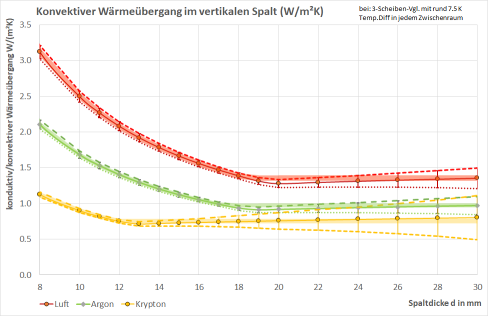 Abb. 1: Wärmedurchlasskoeffizient durch einen geschlossenen vertikalen Spalt mit verschiedenen Füllgasen: Luft, Argon und Krypton
Abb. 1: Wärmedurchlasskoeffizient durch einen geschlossenen vertikalen Spalt mit verschiedenen Füllgasen: Luft, Argon und Krypton
Weiter zu: Was sind Wärmebrücken? 🌡️
Zurück zum Grundkurs Bauphysik Wärme - Übersicht 🌡️