Mehr Details der Temperaturmessung im Wandquerschnitt

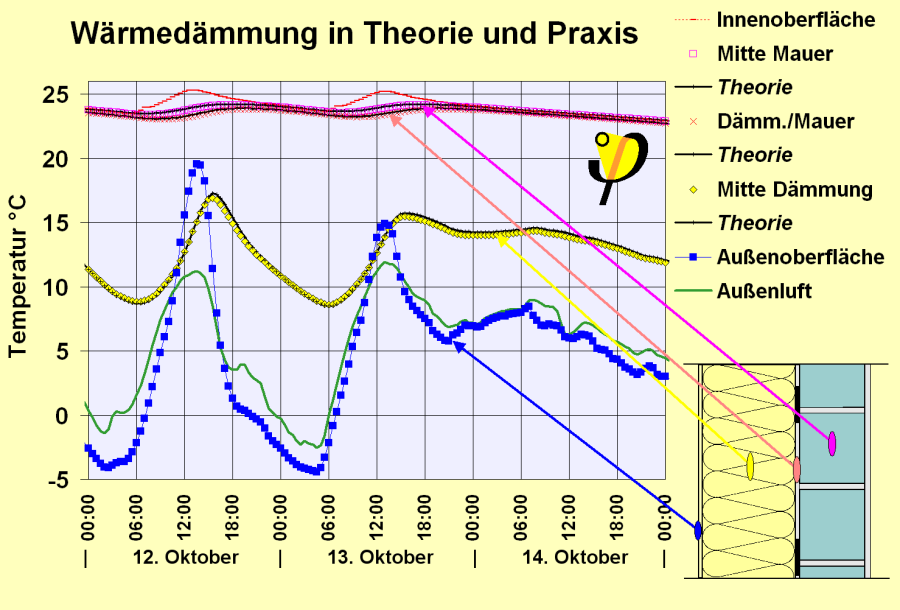
Die Messergebnisse in der westorientierten Außenwand des Passivhauses Darmstadt Kranichstein haben wir unter "Wirkt die Wärmedämmung wie erwartet?" dargestellt. Dort finden sich auch alle Details zu diesem Wandaufbau, der Genauigkeit der Messung und dazu, wie sich aus dieser Messung die Wirksamkeit der Wärmedämmung prüfen lässt. Das Diagramm mit den Messergebnissen wiederholen wir hier noch einmal um im Folgenden noch eine Reihe weiterer Erkenntnisse damit illustrieren zu können. Das Diagramm zeigt die Messergebnisse bei einer Langzeitmessung¹⁾ auf Oberflächen und innerhalb der Konstruktion bei einer wärmegedämmten Wand. Die Wand selbst ist im Querschnitt in der rechten unteren Ecke dargestellt: Die linke Seite ist außen, die Tragkonstruktion besteht aus einem 175 mm dicken Kalksandsteinmauerwerk (graublau), darauf ist außen eine 275 mm dicke Wärmedämmung aufgebracht, die verputzt ist.

Temperaturmessung in einer wärmegedämmten Außenwand. Die gemauerte Wand bleibt trotz niedriger Außentemperaturen im gesamten Querschnitt warm, weil die Wärmedämmung vor Auskühlung schützt. Die Grafik zeigt viele interessante Details, die im Text näher erläutert werden.

Temperatursensoren befinden sich:

• Knapp unter der Innenoberfläche des Innenputzes (rotes Strichsymbol)
• In der Mitte des Mauersteins (violettes Quadrat)
• Oberfläche zwischen der Dämmung und dem Mauerwerk (hellrotes Kreuz)
• In der Dämmschicht (12 cm unter der Außenoberfläche, gelb gefüllte Raute)
• Knapp unter der Außenoberfläche im Außenputz (blau ausgefülltes Quadrat)
• Außenlufttemperatur (grüne Kurve)²⁾

Für diese Außenwand gibt es ein mit den Abmessungen und Labor-gemessenen Materialkennwerten (wie z.B. Wärmeleitfähigkeiten) erstelltes Computer-Simulationsmodell. Die Simulation beruht auf Fouriers Wärmeleitungsgleichung (zeitabhängige Form). Sie wurde in nur einer Raum-Dimension angesetzt, denn die Wandfläche ist insgesamt recht groß und Wärmebrückeneffekte werden nur in ganz geringem Ausmaß erwartet. Auch wurden keine Temperatur- oder Feuchte-abhängigen Materialeigenschaften verwendet und der Feuchtetransport in der Wand nicht eingekoppelt; es kann leicht abgeschätzt werden, dass die genannten Effekte zwar in einem gewissen Ausmaß in der Wand stattfinden, dass diese sich aber nur geringfügig auf die Ergebnisse auswirken; so geringfügig, dass dies innerhalb der vorliegenden Messgenauigkeit nicht nachweisbar ist³⁾.

Die Ergebnisse der Simulationsrechnung sind bereits im gleichen Diagramm mit eingezeichnet: Es sind die durchgezogenen schwarzen Linien, die sich fast ununterscheidbar mit den Symbolen aus der Messaufzeichnung decken. Nun, da die Aufmerksamkeit darauf gelenkt ist, lässt sich z.B. bei der Kurve mit den gelben Dreiecken zeitweise eine geringfügige Abweichung zwischen der Simulationskurve und den Messwerten erkennen: am 12. Oktober zwischen 13:00 und 18:00 liegen die Werte der Simulation z.B. wenige Zehntel Grad über den Messwerten in der Wand. Wenn spekuliert werden soll, worin diese kleine Abweichung vielleicht begründet ist: Dafür gibt es eine große Zahl von Möglichkeiten, zwischen denen ohne nähere Untersuchung nicht entscheiden werden kann: Recht wahrscheinlich ist, dass die Wärmekapazität in der Dämmschicht am Ort des Sensors anders⁴⁾ ist, als in der Simulation angesetzt: der Sensor selbst hat eine gewisse Wärmekapazität und er wurde zwischen zwei Dämmplatten mit Mörtel eingeklebt; wir wissen nicht, wieviel Mörtel das genau war - und der erkennbare Effekt ist auch so gering, dass durch die mangelnde Detailerhebung keine Aufsehens erregenden Abweichungen resultieren. Es kann aber auch sein, dass sich der Sensor effektiv einfach ein paar Millimeter weiter außen befindet als im Modell angesetzt: Änderungen der kapillar aufgenommenen Wärme könnten eine Rolle spielen oder auch kleine Wassermengen in Phasenübergängen. Was auch immer die Abweichung verursacht - der Effekt ist so klein, dass wir recht daran taten, das einfache thermische Modell zu verwenden, wie es ober beschrieben wurde. Die Diskussion hier zeigt dann, dass die Fourier-Gleichung die Wärmestrom- und Temperurentwicklung in diesem Aufbau auch in allen Details ziemlich genau widerspiegelt. Die Untersuchung bestätigt damit die Validität der in der Bauphysik eingeführten Gleichungen.

Konsequenz: Ein wichtiger Schluss aus dem gerade dargestellten Vergleich ist, dass das Computer-Simulationsmodell geeignet ist, z.B. die Werte für die Temperaturen genauso zuverlässig zu liefern, wie die Messungen. Das hat weitreichende praktische Konsequenzen: Z.B. können jetzt auch Temperaturen an anderen Stellen des Querschnittes, z.B. in 3⁄4-Position in der Dämmlage berechnet werden - dort gibt es keine Sensoren und dennoch können wir uns auf eine solche Berechnung verlassen. Auch die Temperaturen in in Zeiträumen, in denen die Messung ausgefallen war oder an anderen Orten mit anderem Temperaturverlauf z.B. der Außentemperatur können auf Grund dieser Validierung zuverlässig berechnet werden. Schließlich kann das Modell z.B. in eines mit nur noch 12 cm Dämmschichtdicke geändert werden und wir können erwarten, das es dann zuverlässig das veränderte Temperaturprofil berechnen lässt. Fast noch wichtiger: Mit dem bestehenden Modell können nicht nur die Temperaturen, sondern auch die inneren Energien der Bauteilschichten berechnet und die vorliegenden örtlichen Wärmströme bestimmt werden: Das erlaub wiederum eine weitaus genauere Berechnung des Wärmeverlustes durch diese Wand durch zeitliche Integration der Wärmeströme knapp unter der inneren Oberfläche.

Anmerkung: Dass wir den Vergleich Simulation/Messung hier als erstes aufführen, hat gute Gründe. Zum einen zeigt dies, wie gut die anerkannten Gesetze der Bauphysik in der Lage sind, die Realität zuverlässig abzubilden. Für die Planung von Neubauten oder Sanierungen sind wir ohnehin auf den Rechenweg angewiesen: Bevor das Gebäude gebaut oder die Maßnahme ausgeführt wurde, lässt sich das thermische Verhalten im konkreten Fall trivialerweise nicht nachmessen. Zuverlässige rechnerische Ansätze sind hier unverzichtbar. Aber auch für viele der im vorigen Abschnitt beschriebenen Anwendungen der Simulation bis hin zu einer korrekten Auswertung der Energiebilanzen ist ein validierter Rechengang nicht nur hilfreich, sondern oft unersetzlich⁵⁾: „Es gibt nichts Praktischeres als eine gute Theorie“(Immanuel Kant).

Die Kurve mit dem blauen Quadrat ist die Temperaturentwicklung an der äußeren Oberfläche - also auf dem Außenputz. Das erste, was hier unmittelbar auffällt, sind die beiden Temperaturspitzen gegen 13:30 am 12. Oktober und 12:30 am Folgetag (Zeitangaben hier in UTC universal time, d.h. Sonnenzeit -2,5 h; es ist somit am 12. Oktober um ca. 16:00 örtliche Sonnenzeit). Die Erklärung ist hier unmittelbar einleuchtend: an diesen Tagen schien die Sonne und die Westwand bekam am Nachmittag ordentlich solare Einstrahlung ab. Es ist übrigens diese Absorption an Oberflächen, die letztlich auch zur Erwärmung der Außenluft im Verlauf des Tages führt (Grüne Kurve). Die an der Oberfläche aufgenommene Strahlungsenergie wird tatsächlich überwiegend von der Oberfläche, die nun merklich wärmer ist als die Außenluft, nach außen an die Luft und durch thermische Abstrahlung in den Himmel wieder abgegeben. Ein kleinerer Teil ist aber Wärmeverlust-reduzierend wirksam: Die Temperaturdifferenz zwischen innen und außen wird nämlich auf diesem Weg reduziert. Das wird sogar im Diagramm unmittelbar erkennbar: Auch die Temperatur weiter innen in der Dämmschicht steigt nämlich, zeitverzögert, an: mit einem Maximum von über 17 °C kurz nach 16:00 (UTC, am 12.10.). Soweit war das auch intuitiv 'einfach' und auch die Simulation trifft diese Vorgänge alle mit hoher Genauigkeit⁶⁾.

Überraschend ist aber auf den ersten Blick, dass zwischen 00:00 und 10:45 und auch wieder ab 16:00 UTC die Temperatur der Außenoberfläche (blau) niedriger ist als die Außenlufttemperatur! Kann das überhaupt sein oder sind das Messfehler? Das kann (und muss sogar) so sein, diese Abkühlung rührt von der Wärmestrahlungsbilanz der Oberfläche her: Nach den Wärmestrahlungsgesetzen strahlt sie Wärme ab, als Planck'scher Strahler gemäß ihrer Temperatur⁷⁾. Sie nimmt auch Wärmestrahlung auf, nämlich die, die von der Umgebung (ähnlich warm) und aus der Atmosphäre kommt - letztere kommt aber weit überwiegend aus höheren Schichten der Luft, insbesondere von CO₂- und Wassermolekülen dort; dort sind die Temperaturen deutlich geringer und dementsprechend ergibt sich hierdurch ein Netto-Wärmestrahlungsverlust. Im Endeffekt wird die Oberfläche hier kälter als die Umgebungsluft, im Oktober bereits über die meiste Zeit des Tages. Dieser Verlust hält über lange Zeiträume an und in der Summe übersteigt er (an diesen Tagen, aber auch generell in der kalten Jahreszeit) die nur kurzzeitig auftretenden passive solaren Gewinne.

Auch das ist alles in ausgezeichneter Übereinstimmung mit der bauphysikalischen Theorie.

Im Diagramm nimmt die Temperatur der Mauersteinwand etwa ab 9:00 am 12. Oktober zwar langsam, aber bis rund 18:00 ebenfalls zu. Oft soll das als Wirkung des Eintrags der Strahlung auf die Außenoberfläche interpretiert werden. Das ist aber ein Irrtum und dies kann auch wieder direkt aus den Temperaturverläufen abgelesen werden.

Schauen wir sorgfältig hin:

Beweis 'a': Auch am 12.Oktober werden die Schichten außerhalb der Mauerwand schon ab der „Mitte der Dämmung“ den ganzen Tag über niemals wärmer als 20°C. Die gemauerte Wand auf der Innenseite hat aber immer und in allen Schichten Temperaturen über 22°C; selbstverständlich können diese immer wärmeren inneren Wandschichten nicht von einem niedrigeren Temperaturniveau aus erwärmt werden. Dieser Wärmeeintrag kann somit nicht von außen kommen.

Beweis 'b': Aber woher kommt die zusätzliche Energie denn dann? Schauen wir nochmals genauer hin: Schon ab ca. 7:00 steigt die Temperatur im Innenputz (rote Strichsymbole) und sie liegt ab diesem Zeitpunkt bis etwa 21:00 dauerhaft über der Temperatur im gesamten Rest der Wand. Der erwärmte Innenputz gibt daher Wärme an die tiefer liegenden Wandschichten ab. Und diese nehmen dann ebenfalls in der Temperatur zu, und zwar zeitlich in der Reihenfolge, dass zuerst die „Mitte der Mauersteinwand“ nachzieht (ab 9:00) und erst danach (ab 11:00) auch die äußerste Schicht der Mauer. Die Energie kommt also von innen. Aber warum erwärmt sich denn der Innenputz? Das ist einfach zu verstehen, denn ab ca. 6:00 (UTC) strahlt passiv solare Energie durch die großen Südfenster in diesen Raum ein. Die wird an den raumseitigen Oberflächen der Möbel und Bauteile absorbiert und erwärmt diese; von dort gelangt die Wärme über Wärmestrahlungszufuhr (schnell!) auch an die Innenoberfläche des Innenputzes, wenn dieser nicht zeitweise sogar selbst von der Besonnung getroffen wird.

Dieser Effekt der durch die Fenster eingestrahlten passiv solaren Energie ist im Innenraum deutlich wirksam, er liefert sogar die gesamten Wärmströme nach, die immer noch über die Außenbauteile verloren gehen, bis zum Ende des 13. Oktobers haben die Temperaturen im Inneren kaum abgenommen. Ab dem 14. Oktober dann schon - das ist ein offensichtlich dauerhaft trüber Tag, passiv solare Erwärmungseffekte sind da auf den ersten Blick nicht erkennbar.

Fazit zur Beobachtung (3): In der kalten Jahreszeit sind die passiv solaren Gewinne durch transparente Bauteile, wie z.B. die Fenster, weitaus bedeutsamer als evtl. Absorption an Außenoberflächen opaker Bauteile. Und auch das ist wieder in voller Übereinstimmung mit dem aus den anerkannten Regeln der Bauphysik zu Erwartenden: Mit der unter (1) beschriebenen Simulation lassen sich die einzelnen Wärmeströme zwischen je zwei Schichten sogar quantifizieren; dabei ergeben sich sowohl die jeweils richtigen Vorzeichen (in der Mauerwand: Wärmestrom immer und in allen Schichten von innen nach außen) als auch die für die Energiebilanz korrekten Beträge der Energieflüsse.

Die gemauerte Wand aus KS-Vollsteinen (24 cm) hat eine hohe Wärmekapazität, bei einer Rohdichte von 1800 kg/m³ und einer spezifischen Wärmekapazität von 0,94 kJ/kg/K ergeben sich rund 112 Wh/(Km²); die meisten heute verbauten Außenbauteile haben ein niedrigeres Wärmespeichervermögen⁸⁾. Die Wärmekapazität dämpft die Amplitude des täglichen Temperaturgangs. In unserem Fall sind das rund 0,9 K an einem klaren Tag mit Solareinstrahlung.

Nun wissen wir schon aus der Betrachtung unter "wirkt der Wärmeschutz?", dass ein so hoher Tagestemperaturgang der Innenseite NICHT durch die wechselnden Temperaturen auf der Außenoberfläche des Bauteils zurückzuführen ist; selbst dann nicht, wenn das Bauteil praktisch keine Wärmekapazitäten hätte. Das quantifizieren wir hier noch einmal.

Ohne Wärmekapazitäten würde sich das Bauteil jeweils sofort auf die zu einer neuen Außenoberflächen-Temperatur zugehörige Gleichgewichts-Innentemperatur einstellen: Diese ergibt sich aus dem Verhältnis des inneren Wärmeübergangswiderstandes zum Wärmedurchlasswiderstand bis zur Außenoberfläche. Beide Werte kennen wir aus dem stationären Fall, sie betragen $R_{si}=$ 0,16 m²K/W und $R_{A}=$ 7,49 m²K/W; d.h., die Temperatur-Schwankung⁹⁾ auf der Innenoberfläche beträgt für den absoluten Leichtbau-Fall 2,12% der äußeren Amplitude¹⁰⁾. Da am 12. Oktober die minimale Außenoberflächentemperatur -4,1 °C beträgt, die maximale 19,6 °C (unter voller Solarlast), beträgt die Amplitude auf der Außenseite immerhin fast 12 K. Auf der Innenoberfläche würden wir davon rund 0,25 K wahrnehmen¹¹⁾: Das ist ein für Personen kaum wahrnehmbarer Unterschied. Dieser Wert 0,25 K ist erheblich geringer ist als die oben dokumentierte gemessene Amplitude von rund 0,9 K. Die entscheidende Ursache für diese Schwankung muss eine andere sein, und wir wissen auch schon, dass es die im Tagesverlauf stark schwankende von innen auf die Oberfläche zugeführte Strahlungswärme ist.

Auch das können wir mit den Messdaten nun quantifizieren: Die Zunahme an thermischer Energie in der gemauerten Wand beträgt am sonnigen 12. Oktober insgesamt 91,1 Wh; diese Zustrahlung findet zwischen 5:30 (UTC) und 16:30 statt, das sind 11 Stunden¹²⁾. Die mittlere zugestrahlte Leistung beträgt daher durchschnittlich rund 8,8 W/m² Bauteiloberfläche; bei den gegebenen Gesamtoberflächen im Raum sind das immerhin rund +680 Watt freie Wärmezufuhr über diesen Zeitraum. Kann das stimmen? Wir wissen, dass die Verglasungsfläche in diesem Raum 4,41 m² beträgt; bei einem g-Wert von rund 0,5 und einem Minderungsfaktor (Verschattung, Einfallswinkel, Schmutz) von 0,55 ergeben sich an einem klaren Oktobertag rund 580 Watt durchschnittlicher Solareintrag in diesen Raum. Das sind rund 100 Watt weniger als die eben grob ermittelte Zunahme der thermischen Energie: Das kann tatsächlich in etwa der Wert der im Raum freigesetzten internen Wärmequellen sein, wenn sich im Arbeitszimmer in diesem Zeitraum überwiegend eine Person aufgehalten hat¹³⁾.

Kommen wir zurück auf die Wirkung der Wärmekapazität: die ist, zusammen mit den Kapazitäten der anderen Bauteile, die an diesen Raum grenzen, bereit, Strahlung und andere unregelmäßig anfallenden Wärmequellen in diesem Raum aufzunehmen und zu einem späteren Zeitpunkt wieder abzugeben. Das hat im konkreten Fall zu einer Temperaturamplitude an der inneren Oberfläche von etwa 0,9 K geführt - ein noch akzeptabler Wert, was die Veränderungen im Behaglichkeitsfeld angeht. Wenn statt des schweren Vollsteins nun für die gleiche Mauersteinwand ein porosiertes Material verwendet worden wäre, dann würde sich die verfügbare Wärmekapazität etwas reduzieren. Die Temperaturamplitude, die durch die passiv solare Energiezufuhr verursacht wird, würde sich dadurch erhöhen: Wir haben das im Gesamtmodell simuliert und kommen dann auf einen neuen Wert der Temperaturamplitude an der Innenoberfläche dieser Wand von etwa 1,6 K. Diese Schwankung ist spürbar höher als in der tatsächlich vorliegenden Situation und dann von den Bewohnern bereits deutlich wahrnehmbar: Allerdings liegt der überwiegende Teil der Wärmekapazitäten in diesem Raum bei den Innenbauteilen - das dämpft den Effekt auf die wahrnehmbare operative Temperatur, zu der eine einzelne Oberfläche nur in ihrem jeweiligen Sichtbarkeitsverhältnis beiträgt; das liegt hier bei nur einem Fünftel für den Arbeitsplatz. Dadurch wird auch diese Auswirkung am Ende wieder weitgehend unbedeutend.

Das Zusammenspiel. Durch die Dämmung der Mauersteinwand auf der Außenseite wird diese wärmetechnisch gesehen zu einer „innen liegenden“ Wand, d.h., die Temperaturen in diesem Bauteil schwanken auf Grund der inneren Einflüsse um die Raumtemperatur herum. Dadurch bedingt kann hier der gesamte Querschnitt dieser Mauer effektiv als Wärmekapazität genutzt werden: Eben, als ob dies eine Innenwand wäre. Für eine derart gut gedämmte Mauersteinwand zählt die Wärmekapazität des Aufbaus effektiv mit zur inneren Wärmekapazität des Gebäudes - sie kann tagsüber überschüssige Wärme aufnehmen und nachts wieder dem Raum zuführen. Das hilft sowohl im Sommer als auch im Winter für eine Vergleichmäßigung des Temperaturgangs und trägt so zur Behaglichkeit im Raum bei. Wir konnten auch hier eine Zusammenhang erneut empirisch am gemessenen Beispiel illustrieren, der in unserer Passipedia-Seite zur effektiven inneren Wärmekapazität behandelt wurde: „Wärmespeicherung wird durch Wärmedämmung erst richtig wirkungsvoll.“

Noch einmal festhalten sollten wir aber Folgendes: Die Wärmekapazität ist nicht selbst eine Wärmequelle - alle Energie, die aus der Kapazität entnommen wird, muss dieser zunächst einmal zugeführt worden sein. Das führt zur Ermöglichung einer Verlagerung von überschüssig zugeführter Energie auf einen späteren Zeitpunkt. Inwieweit das im konkreten Fall den Energieverbrauch reduziert, hängt vor allem davon ab, wie „überflüssig“ die Energie zum Zeitpunkt der Beladung wirklich war. In unserem konkreten Fall liegen die Innentemperaturen im Heizzeitraum¹⁴⁾ nie über der Komfortgrenze, auch wenn da einmal die Sonne in vollem Ausmaß durch die Fenster scheint. Selbst mit geringeren Wärmekapazitäten als den hier vorliegenden würde sich daran im Winter nichts ändern - die passiv solaren Gewinne in diesem Gebäude sind und bleiben zu nahezu 100% nutzbar. Die Wirkung der Wärmekapazitäten beschränkt sich damit auf den hier dargestellten ausgleichenden Einfluss auf die Tagesschwankungen der Temperaturen im Sommer und in der Übergangszeit¹⁵⁾; dafür ist diese schwere gemauerte Wand tatsächlich von Vorteil, wie wir gesehen haben.