====== Beheizter Keller ======

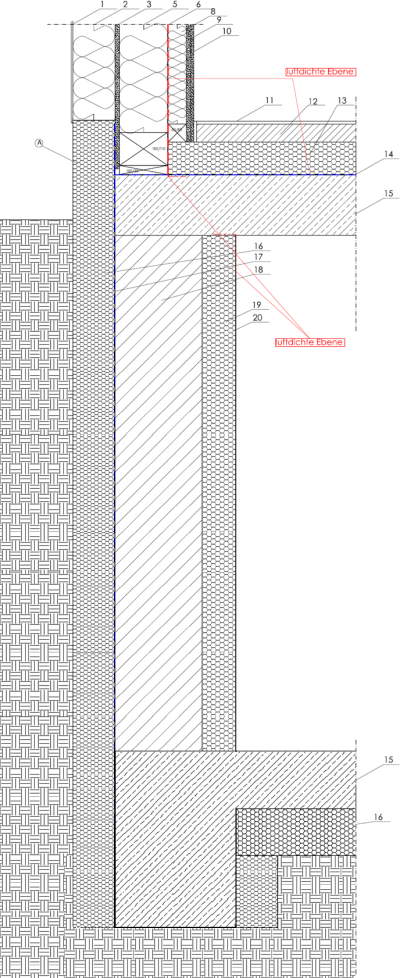
In DIN EN ISO 13370 bzw. DIN EN ISO 10211 wird für ein beheiztes Kellergeschoss nur ein Ψ-Wert ermittelt. Dieser erfasst den oberen Kellerdecken-Anschluss und den Anschluss der Kellerwand an die Keller-Bodenplatte. Auch für das Erdreichblatt des [[planung:energieeffizienz_ist_berechenbar:energiebilanzen_mit_dem_phpp|PHPP]] ist es ausreichend, $\Psi_{gesamt}$ einzugeben (als Perimeter-Wärmebrücke). Alternativ können die beiden Anschlüsse ($\Psi_{oben}$ und $\Psi_{unten}$) getrennt auf das Kriterium der Wärmebrückenfreiheit überprüft werden.

{{ :picopen:beheizter_keller_abb_1.png?direct&400 |}}

Das Vorgehen zur Ermittlung der angesprochenen Wärmebrückenverlustkoeffizienten wird nachfolgend gezeigt. An dieser Stelle ist zu erwähnen, dass im Erdreichblatt des [[planung:energieeffizienz_ist_berechenbar:energiebilanzen_mit_dem_phpp|PHPP]] für die Keller-Bodenplatte sowie für die Kellerwand, unter Berücksichtigung des Erdreiches, U-Werte durch die Näherungsfunktionen der DIN EN ISO 13370 bestimmt werden. Somit kann auch für beheizte Keller Option A bzw. Option B angewendet werden. Im Rahmen einer Bausystem-Zertifizierung sollte jedoch auch hier Option B für die Bestimmung der Ψ-Werte angewendet werden.

{{ :picopen:beheizter_keller_abb_2.png?direct&400 |}}

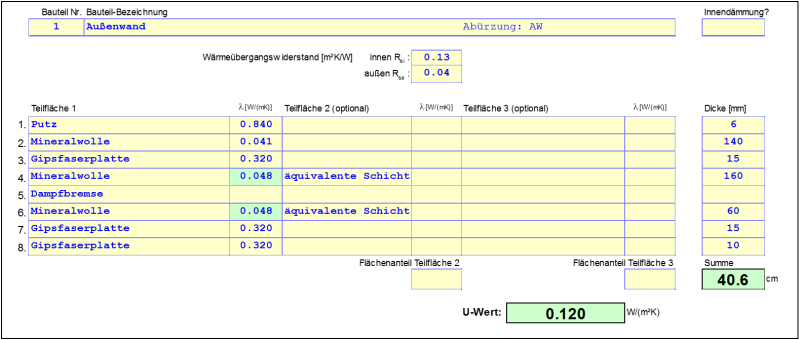
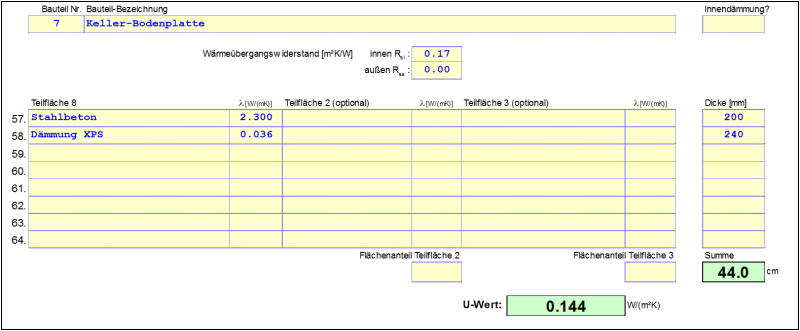
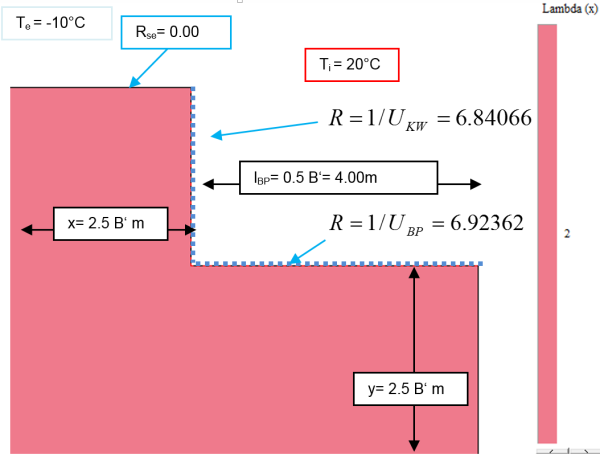
Nach der Abbildung oben lassen sich die U-Werte der für die Ψ-Wert Ermittlung relevanten Bauteile wie folgt bestimmen:

{{ :picopen:beheizter_keller_abb_3a.png?direct&800 |}}

{{ :picopen:beheizter_keller_abb_3b.png?direct&800 |}}

{{ :picopen:beheizter_keller_abb_3c.png?direct&800 |}}

\\
===== Berechnungsmodelle =====

<WRAP centeralign>
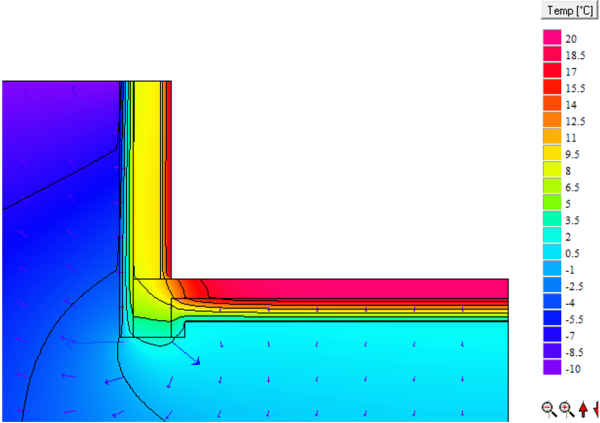
**Leitwertbestimmung** 
$
\Large{L_{2d}}
$
</WRAP>

{{ :picopen:beheizter_keller_abb_4a.png?direct&600 |}}
\\
{{ :picopen:beheizter_keller_abb_4b.png?direct&600 |}}

<WRAP centeralign> 
$$
\large{\dot{q} = 38{,}123 \, \dfrac{\text{W}}{\text{m}}}\\
$$
</WRAP>

<WRAP centeralign>
$$
\large{L_{2d} = \dfrac{\dot{q}}{T_i-T_e} = \dfrac{38{,}123}{30} = 1{,}2708 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}}}
$$
</WRAP>

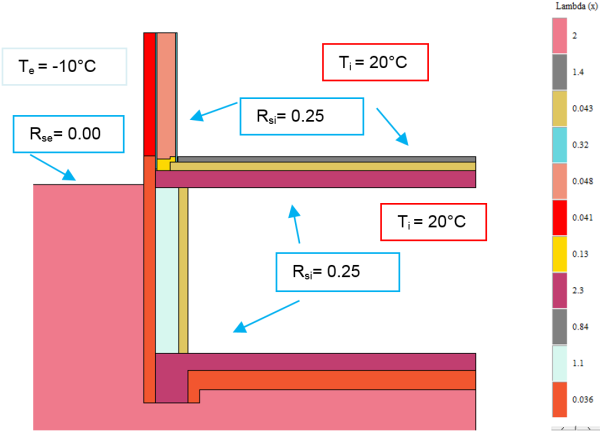
$L_{2d}$ ist damit berechnet. Um den Ψ-Wert ermitteln zu können, müssen noch die Leitwerte der Außenwand, der Kellerwand und der Kellerbodenplatte ermittelt werden. Der Leitwert der Außenwand kann auch hier einfach aus dem U-Wert und der angesetzten Länge ermittelt werden. Die Leitwerte der Kellerwand und der Keller-Bodenplatte müssen nach Option B, also durch eine zusätzliche Berechnung, ermittelt werden. Dazu werden analog zur Bodenplatte die erdberührten Bauteile durch ihren Übergangswiderstand abgebildet.

<WRAP centeralign>
**Leitwert der Keller-Bodenplatte und Kellerwand** 
$
\Large{L_{BP,KW}}
$
</WRAP>

{{ :picopen:beheizter_keller_abb_5a.png?direct&600 |}}
\\
{{ :picopen:beheizter_keller_abb_5b.png?direct&600 |}}


<WRAP centeralign> 
$$
\large{\dot{q} = 22{,}190 \, \dfrac{\text{W}}{\text{m}}}\\
$$
</WRAP>

<WRAP centeralign>
$$
\large{L_{BP,KW} = \dfrac{\dot{q}}{T_i-T_e} = \dfrac{22{,}190}{30} = 0{,}7397 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}}}
$$
</WRAP>

\\
<WRAP centeralign>
**Leitwertermittlung der Außenwand** 
$
\Large{L_{AW}} 
$
</WRAP>


<WRAP centeralign> 
$$
\large{U_{AW} = 0{,}1205 \, \dfrac{\text{W}}{\text{m}^2 \cdot \text{K}}}
$$
</WRAP>

<WRAP centeralign>
$$
\large{L_{AW} = l_{AW} \cdot U_{AW} = 1{,}83 \cdot 0{,}1205 = 0{,}2205 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}}}
$$
</WRAP>

\\
<WRAP centeralign>
**Ψ-Wert Ermittlung (Gesamt)** 
</WRAP>

<WRAP centeralign> 
$$
\Psi_{gesamt} = L_{2d}-L_{AW}-L_{BP,KW}=1{,}2708-0{,}2205-0{,}7397=0{,}311 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}}
$$
</WRAP>

\\
In der Praxis sollten auch hier vorgefertigte Excel-Vorlagen zur Bestimmung der Ψ-Werte verwendet werden. Man kann dort die Wärmeströme und die notwendigen Längen eintragen und erhält direkt den gesuchten Ψ-Wert als Ergebnis:

{{ :picopen:beheizter_keller_abb_6.png?direct&500 |}}

Anmerkung: Es liegt also kein wärmebrückenfreier Anschluss vor. In dem gegebenen Beispiel ist es relativ deutlich, dass der Kellerwand-Anschluss an die Keller-Bodenplatte nicht ideal ausgeführt ist. Dem Auftraggeber würde man empfehlen, auch unter dem Fundament zu dämmen (vgl. AkKP 35). Unabhängig davon stellt sich die Frage, wie es mit dem oberen Anschluss aussieht. Kann der Geschossdecken-Anschluss als wärmebrückenfrei angesehen werden? Streng genommen kann man die beiden Anschlüsse nicht voneinander getrennt betrachten. Das Erdreich stellt eine thermische Verbindung zwischen der Kellerwand und der Bodenplatte her. So beeinflusst der Wärmestrom durch die Bodenplatte den Wärmedurchgang durch die Kellerwand und umgekehrt. In den meisten Fällen befindet sich der Anschluss Kellerwand - Außenwand jedoch nahe an oder sogar über Oberkante Gelände. Damit sind die Wechselwirkungen gering und eine für die praktische Anwendung wünschenswerte, getrennte Angabe von $\Psi_{unten}$ und $\Psi_{oben}$ ist gerechtfertigt.
Wir schlagen vor, einheitlich zunächst den unteren Anschluss zu berechnen. Möglich wäre auch der umgekehrte Weg, was eine (meist nur geringfügig) andere Aufteilung von $\Psi_{gesamt}$ auf $\Psi_{unten}$ und $\Psi_{oben}$ zur Folge hätte.

<WRAP centeralign>
**Leitwertbestimmung** 
$
\Large{L_{2d}}
$
</WRAP>

{{ :picopen:beheizter_keller_abb_7a.png?direct&600 |}}
\\
{{ :picopen:beheizter_keller_abb_7b.png?direct&600 |}}


<WRAP centeralign> 
$$
\Large{\dot{q} = 29{,}588 \, \dfrac{\text{W}}{\text{m}}} \\
$$
</WRAP>

<WRAP centeralign>
$$
\large{L_{2d} = \dfrac{\dot{q}}{T_i-T_e} = \dfrac{29{,}588}{30} = 0{,}9863 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}}} 
$$
</WRAP>

Der Leitwert $L_{BP,KW}$ ist bereits aus der Gesamtermittlung bekannt. Für den Kellerwand-Anschluss an die Bodenplatte resultiert folgender Ψ-Wert:

<WRAP centeralign>
**Ψ-Wert Ermittlung (unterer Anschluss)** 
</WRAP>

<WRAP centeralign> 
$$
\large{\Psi_{unten} = L_{2d}-L_{BP,KW}=0{,}9863-0{,}7397 = 0{,}247 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}}}
$$
</WRAP>

Den Ψ-Wert für den oberen Anschluss kann man nun aus der Differenz zwischen $\Psi_{gesamt}$ und $\Psi_{unten}$ berechnen. Damit ist in $\Psi_{oben}$ der Einfluss des unteren Anschlusses enthalten.

<WRAP centeralign>
**Ψ-Wert Ermittlung (oberer Anschluss)** 
</WRAP>

<WRAP centeralign> 
$$
\large{\Psi_{oben} = \Psi_{gesamt}-\Psi_{unten} = 0{,}311-0{,}247 = 0{,}064 \, \dfrac{\text{W}}{\text{m} \cdot \text{K}}}
$$
</WRAP>

Der Kellerdecken-Anschluss ist ebenfalls nicht wärmebrückenfrei. 

\\
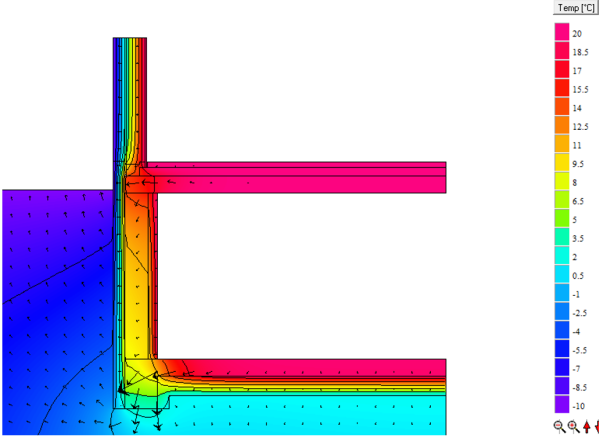
===== Bestimmung der Oberflächentemperatur =====

Zur der Bestimmung der minimalen Oberflächentemperatur und des $f_{Rsi}$-Faktors kann in diesem Fall wie bei jeder anderen Wärmebrücke vorgegangen werden.

<WRAP centeralign>
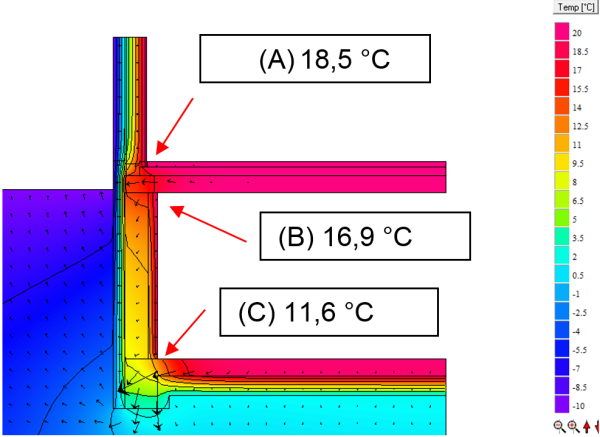
**Bestimmung der minimalen Oberflächentemperatur und von** 
$
\Large{f_{Rsi}} 
$
</WRAP>



{{ :picopen:beheizter_keller_abb_8a.png?direct&600 |}}


{{ :picopen:beheizter_keller_abb_8b.png?direct&600 |}}

<WRAP centeralign> 
$$
\large{f_{Rsi,A} = \dfrac{18{,}5-(-10)}{20-(-10)} = 0{,}94}
$$
</WRAP>

<WRAP centeralign>
$$
\large{f_{Rsi,B} = \dfrac{16{,}9-(-10)}{20-(-10)} = 0{,}89}
$$
</WRAP>

<WRAP centeralign>
$$
\large{f_{Rsi,C} = \dfrac{11{,}6-(-10)}{20-(-10)} = 0{,}72}
$$
</WRAP>

**Anmerkung!** //Bereiche, die nahe an der Erdoberfläche liegen, unterliegen größeren Temperaturschwankungen als solche, die weiter von der Oberfläche entfernt sind. Die stationär ermittelten Oberflächentemperaturen von weiter entfernten Bereichen sind daher weniger aussagekräftig, aber in der Regel auf der sicheren Seite, da die dazu nötigen Randbedingungen in der Realität monatelang anliegen müssten. Sind genauere Oberflächentemperaturen gefragt, können zwei- oder dreidimensionale instationäre Berechnungen die Lösung sein.//

===== Siehe auch =====
  * [[grundlagen:bauphysikalische_grundlagen:waermebruecken:wbberechnung]]
  * [[grundlagen:bauphysikalische_grundlagen:waermebruecken:wbberechnung:erdreich:vorgehensweise]]
  * [[grundlagen:bauphysikalische_grundlagen:waermebruecken:wbberechnung:beispiele:start]]